Mathematics
H110
Fall, 2003
CourseWeb
H110 Web Page
Enrollment
Information
Office: 510 642 0648
Fax: 510 642 8204
email:
ribet@math.berkeley.edu
Syllabus
Matrices, vector spaces, linear transformations, inner
products, determinants.
Eigenvectors. QF (sic.) factorization. Quadratic forms and Rayleigh's
principle. Jordan canonical form, applications. Linear functionals.
This
catalog description
gives you some idea of what we might cover.
If you look at the assignments
for
the course
that I taught
in 2002-2003, you'll get a sense of the set of topics that
can be covered in a non-honors version of Math 110. We will certainly
do things
a bit differently in H110. In particular, the Jordan canonical form
should be well within our reach.
Textbook
Linear
Algebra, 4th ed., by
Stephen H. Friedberg 
,
Arnold J. Insel
,
Lawrence E. Spence
.
Recommended Reading:
There are quite a few good
linear algebra books in circulation; see the
textbook
lists for some examples.
Whenever you feel stuck when reading our
text,
feel free to consult alternative treatments.
Reading several discussions
of one topic is often illuminating.
One excellent book is
Linear Algebra Done Right
by
Sheldon Axler
.
This book was based partly on ideas from
Axler's article
Down with Determinants!,
which you might enjoy reading.
Graduate Student Instructor
The GSI for all Math 110 classes is
Alexander J. Diesl.
He will hold Math 110
office hours
in
891 Evans
as follows:
- Wednesday 10-12 AM and 1-4 PM
- Thursday 8-11 AM and 12-2 PM
- First Midterm: September 29, 2003,
Questions and solution sketches.
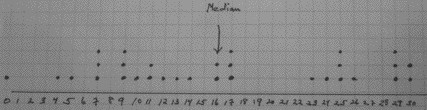
Distribution of scores -- note the gap between 17 and 23:
- Second Midterm: November 3, 2003.
Questions and solution sketches.
Distribution of scores -- sorry!
- Final Exam:
Tuesday, December 16, 2003, 5-8PM (Exam group 17)
in 70 Evans.
Questions and solution sketches.
Distribution of scores:
Recall that students were asked to choose 6
out of the 8 problems. Despite indications to the contrary on the
exam paper, all problems had
equal weight: 6 points. The maximum score
on the final was thus 36.
You might possibly find
last year's tests
useful in preparing for exams.
Grading
The
H113 grading scheme
for last semester worked out pretty well.
(I think so, anyway!)
I tried to clone it.
The intention was to make the course components count as
follows:
Homework 25%, midterms 15% each, final 45%.
This class had 24 registered students (including one concurrent
enrollment student); 23 students took the final exam.
The grades for these students turned out
as follows: 13 A's (including some A+
and A- grades), 9 B's, 1 C.
See the grading table for more information.
Homework Assignments
Homework will be assigned weekly.
Because the
Math 110 GSI
will be available to answer your questions on Wednesday and
Thursday of each week, most homework
assignments will be due on Friday.
When you prepare your homework,
write carefully, in complete
English sentences. Explain what you are doing, even if the
problem is essentially a computation. Remember that the
person
grading the homework
doesn't live inside your brain;
when your homework is graded, your insights are represented only by
the paper that you submitted.
Please staple your assignment together before you submit it; we don't
want pages to get lost!
See John Voight's
Math H110 Web page
for homework solutions.
- Assignment due August 29:
[mean = 16, standard deviation = 3]
- § 1.1:
7
- § 1.2:
1 (all parts),
8, 10, 16, 21
- § 1.3:
1 (all parts),
2h, 8 (all parts), 11, 13, 19, 20, 23
- Assignment due September 5:
[mean = 18, standard deviation = 2]
- § 1.4:
12, 13, 14, 15, 16 ,17
- § 1.5:
7, 8, 9, 10, 11, 13, 14, 15, 18
- Assignment due September 12:
[mean = 16, standard deviation = 4]
- Let F be a finite field, i.e., a field with a finite number of elements.
Find a formula for the number of bases of the vector space F^n (n-space
over F). The number in question should depend in a simple way on n and
the number of elements of F.
- Suppose that V is a vector space over F with basis S and that E is
a subfield of F. (Think of E as a field contained in F; an example
would be R inside C.) We may view F an an E-vector space
in a natural way: the "scalars" in E act on the "vectors" in F by
multiplication. Suppose that T is a basis of F as an E-vector space.
Show that the products ts with s in S and t in T form a basis of V as
an E-vector space.
- § 1.6:
7, 8, 12, 13, 20, 21, 24, 26, 29, 31, 32
- Assignment due September 19:
[mean = 15, standard deviation = 3]
- § 2.1:
13, 14, 17, 21, 26, 27, 31, 32, 35
- § 2.2:
12, 13
- § 2.3:
12, 15, 16, 17
- Suppose that X and W are subspaces of a vector space V. Assume that
V is the internal direct sum of X and W; this means (1) that the intersection
of X and W is {0} and (2) that every vector in V is a sum x+w with x in X
and w in W. Consider the map from X to V/W that sends x in X to the coset
x + W in V/W. Prove that this map is an isomorphism of vector spaces.
- Assignment due September 26.
[mean = 15, standard deviation = 6]
On the first line, ignore the reference to problem 10 of
§ 2.6. This problem appears on the last line as well; do it only
once!
- Assignment due October 3:
[mean = 18, standard deviation = 2]
- § 3.2:
14,
18, 19, 21, 22
[Watch out for problem 18, which is stated incorrectly in the first
printing of the fourth edition. See
the
errata for
the first printing for a correction.]
- § 3.3:
10
- § 4.2:
5, 6, 28, 29
- Assignment due October 10:
[mean = 17, standard deviation = 3]
- § 4.3:
11, 12, 16, 17, 20, 21, 22, 23, 25
- Let n be an integer that is non-zero in F. (For example, if
F is the field of integers mod a prime number p, this means that
n is not a multiple of p.) Show that the identity matrix of size
n cannot be written in the form AB-BA where A and B are square
matrices of size n.
- In the previous problem, what can you say when n=0 in F?
[These last two problems were suggested by
George Bergman.
I've written up a
comment.]
- Assignment due October 17:
[mean = 17, standard deviation = 3]
- Please start
reading
Keith Conrad's
treatment
of a
recent
article
by
Harm Derksen
that appeared in the
American Mathematical
Monthly.
I will lecture on Wednesday, and maybe also on Friday, from this
text.
- Suppose that T is a linear operator on a finite-dimensional F-vector
space V. Suppose that W is a subspace of V that is T-stable in the sense
that T(w) lies in W for all w in W. Show that the formula
v+W |-> T(v)+W can be used to define a linear transformation U
from V/W to V/W. This is the linear map that T induces on V/W.
Prove that the characteristic polynomial of T is the product of the
following two polynomials:
the characteristic polynomial of U and the characteristic polynomial
of the restriction of T to W (thought of as a map from W to W).
- § 5.1:
17, 18, 20, 21
- § 5.2:
20, 21, 22, 23
- Assignment due October 24.
[mean = 18, standard deviation = 3]
- Assignment due October 31.
[mean = 12, standard deviation = 6]
To read about orthogonal polynomials on the Net, you can start
with Chapter 22
of Abramowitz and Stegun
or the
orthogonal
polynomials page of
Eric Weisstein's World of
Mathematics.
- Assignment due November 7:
[mean = 15, standard deviation = 6]
- § 6.2:
10, 12, 13, 14, 15, 16
- § 6.3:
9, 14
- § 6.4:
10, 13, 14
- Assignment due November 14;
I removed §6.5 problem 7 on November 13 and added a solution
for problem 16 on November 18.
[mean = 15, standard deviation = 6]
- Assignment due November 21.
In the first problem, the conditions are that for each *non-zero* x there's
a y such that H(x,y) is non-zero and similarly for each non-zero y.
You can
read the short
Web
biography of James Joseph Sylvester
if you're curious about the person behind the "invariance of inertia"
theorem. Sylvester was apparently the first mathematician to use
the term "matrix" with its current Math 110 meaning; this was
in 1850.
Oh yeah, there's also a
biography
of Marie Ennemond Camille Jordan that you can read at the same
time!
-
Assignment due December 3, 2003
and further review problems.
Anonymous Feedback
Please let me know what I'm doing right and what I'm doing wrong.
Constructive feedback is always welcome;
don't hesitate to propose changes.
You might be inspired by the
comments that were made by
students in Math H113
last semester
and by
those that were made
by the Math 250 students two years ago.
Update:
the comment box is no longer active; school is out.
You can read
the comments that were
submitted for this course during the semester.
In
the course evaluation that
was conducted a few weeks ago:
the instructor received 2 5's, 14 6's, and
7 7's for an average score of 6.22.
Some students thought that the course wasn't sufficiently
challenging, but plenty reported that the course was very
hard.
