OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996-2010
J.A. Sethian
Overview
-
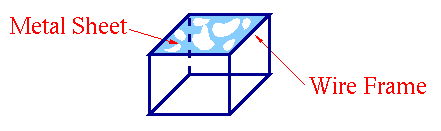
Imagine you are given a square piece of metal, and supposed that the
metal is resting on a square frame. Your job is to design a metal
cover that fits nicely on that frame, but doesn't sag or bend too much.

Imagine trying to build a systematic technique for finding optimal designs. Trial and error is one possibility:
Some of the difficulties with this approach are that it's hard to know where to start cutting holes, it is hard to know how to efficiently characterize the holes, and it is hard to know how to solve the constraint equations which tell the stress on the material given a collection of holes.- First, cut some holes in random places.
- See if the resulting structure violates the constraint requirement.
- If not, try cutting a few more in random places.
An Evolving Interface Approach to Optimal Design
-
Interface methods can be used to find good designs for these sorts of
problems. The central idea is to start with a few holes, and evolve the
boundaries of these holes in ways that remove material, but do not
violate the constraint equations.
Several things are needed:
- Given a bunch of holes, and the boundary constraints on the material, we have to calculate the solution to the stress/strain equations to figure out the amount of bending in the material. This is provided by a version of the Immersed Interface Method.
- With the solution of these equations, we need a way to move the boundaries to a new position which still satisifies the constraint equation and uses less material. This is provided by the level set method.
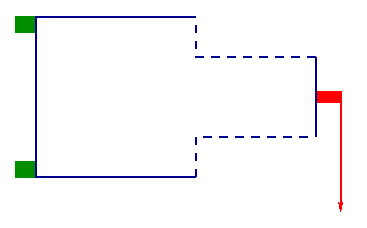
As an example, suppose we start with a "T"-square:
First, we calculate the stresses on the material:- The boundary of the metal sheet is in blue.
- The green blocks are fixed and clamped; the metal sheet cannot bend or sway.
- Straight down at the red block, a load is placed in the direction of the arrow.
- The dashed blue parts of the boundary can move to help build an optimal design.

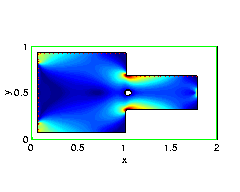
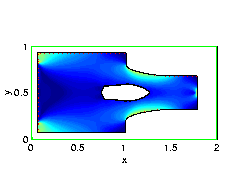
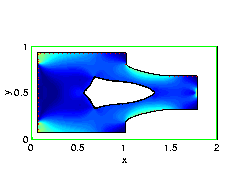

A movie of evolution towards a locally optimal design (79K)
Advantages of this Approach
- There are several advantages to this approach. The first is that we solve the elastic strain equations on a fixed grid through a version of the Immersed Interface Method; doing so avoids many of the complications that come from using distorted and convoluted unstructured meshes. Second, the level set method allows us to perturb the shapes of the interface, without worrying about changes in topology, how many holes are required, etc. The entire method carries over to three dimensions, if desired.
Additional Results
-
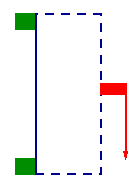
Again, we follow the following convention:
- The boundary of the metal sheet is in blue.
- The green blocks are fixed and clamped; the metal sheet cannot bend or sway.
- Straight down at the red block, a load is applied in the plane of the sheet in the direction of the arrow. Arrow width is proportional to the force (same in all figures), arrow length indicates the tightness of the constraint. A shorter arrow means less yielding is permitted.
- The dashed blue parts of the boundary can move to help build an optimal design.

Movie of locally optimal evolution Movie of locally optimal evolution 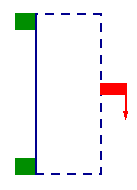
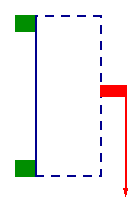
Movie of locally optimal evolution Movie of locally optimal evolution Movie of locally optimal evolution
Details
-
The calculation was performed using a
level set method
to track the motion of
an initial interface, coupled to a version of the Immersed Interface
Method.
Given a design, we first apply an Explicit Jump Immersed Interface
Method (EJIIM) for computing the solutions for a given design shape.
We then use a narrow band level set method to perturb this shape and
progress towards a more fitting design.
In the first step, the EJIIM is applied to the equations of 2D linear elastostatics in the displacement formulation, and problems on arbitrary domains are solved quickly by domain embedding and the use of fast elastostatic solvers. This effectively reduces the dimensionality of the problem by one. One main difficulty is a change of topology as the design is modified. This is dealt with by the Level Set Methodology, which represents the design structure through an embedded implicit function. Once the stresses are found, the level set method is used in the second step to alter the shape, with velocities depending on the stresses in the current design. Criteria are provided for advancing the shape in an appropriate direction, and to correct the evolving shape when given constraints are violated. References
- Sethian, J.A., and Wiegmann, A., Structural Boundary Design via Level Set and Immersed Interface Methods , J. Comp. Phys., 163, 2, Sep 2000, pp. 489-528,
This paper List of downloadable publications
- Sethian, J.A., and Wiegmann, A., Structural Boundary Design via Level Set and Immersed Interface Methods , J. Comp. Phys., 163, 2, Sep 2000, pp. 489-528,