HOME

OVERVIEW

APPLICATIONS

  • Geometry
  • Soap Bubbles
  • Medical Imaging
  • Robotics
  • Fluids
  • Semiconductors
  • Wave Propagation
  • Image Denoising
  • Optimal Design
  • Seismic Analysis
  • Tumor Modeling
  • Optimal Control
  • InkJet Plotters
  • Traveling Salesmen
  • ViscoElastic Flow
  • Pinching Droplets
  • Chemical Pathways

    INTERACTIVE APPLETS

    HISTORY OF THE METHODS/FLOW CHART

    PUBLICATIONS

    EDUCATIONAL MATERIAL

    ACKNOWLEDGEMENTS

    ABOUT THE AUTHOR/CV








    Copyright:
    1996-2010
    J.A. Sethian

    • Optimal Control



    Motivation

    Fast Marching Methods are designed to track a propagating interface, and find the first arrival of the interface as it passes a point. They also are designed for problems in which the speed of propagation is isotropic: this means that standing at any point, you get to move in any direction with the same speed. That speed can change from point to point, but once you dropped in the domain, there's no preferred direction. This was the setting for the problem of robotic navigation, in which we found the optimal path through and around a set of obstacles.

    In optimal control , how much it costs to move depends on both where you are standing and also on the direction in which you chose to move. A good example is sailing: the direction of the wind gives a preferred direction, and your speed depends on which direction you choose. There are many physical examples of this, including preferred directions in the etching of microchips and anisotropic propagation of waves in rock.

    Fast Marching Methods have many desirable qualities.
    • First, they are one-pass methods: rather than iterate over the grid points until one converges to a solution, they allow one to systematically update the points in order so that each point is touched essentially only once. This is because they are built around Dijkstra's Method, which is a one-pass method for finding the cheapest path on a weighted graph of edges and nodes.
    • Second, they are very fast: this systematically ordering allows one to compute the solution in O(N log N) steps, where N is the number of grid points where the solution is requested.


    Unfortunately, the Fast Marching Method won't work in this setting. The answer why has to do with how the method really works. In the Fast Marching Method, just like Dijkstra's method, one systematically updates the solution starting from known values, and works from known territory to unknown spots. At each step, one exploits the fact that the perpendicular (or gradient) back to the front is the direction from which information must come. Mathematically, this means that the characteristics are the same as the gradient.

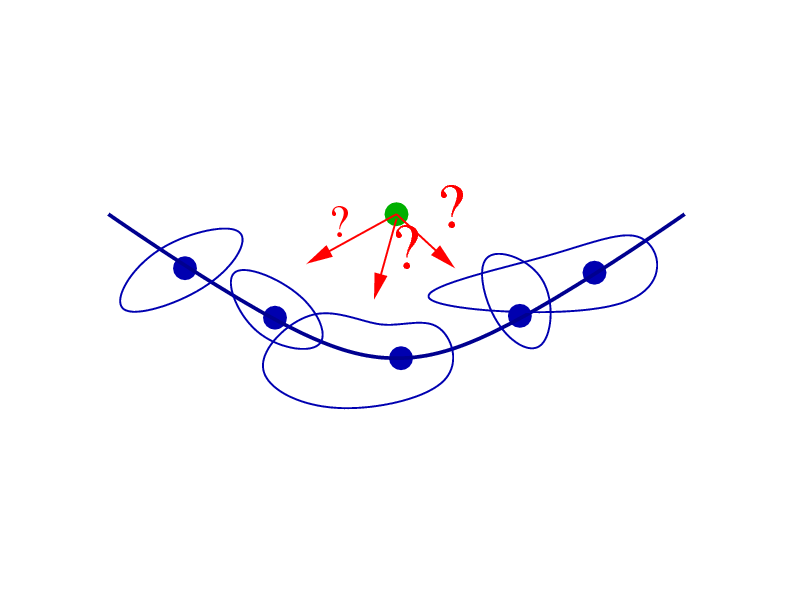
    And this isn't true when the speed is not isotropic. If the speed depends on the direction, then one cannot assume that information always arrives at the green spot along a trajectory perpendicular to the evolving front.
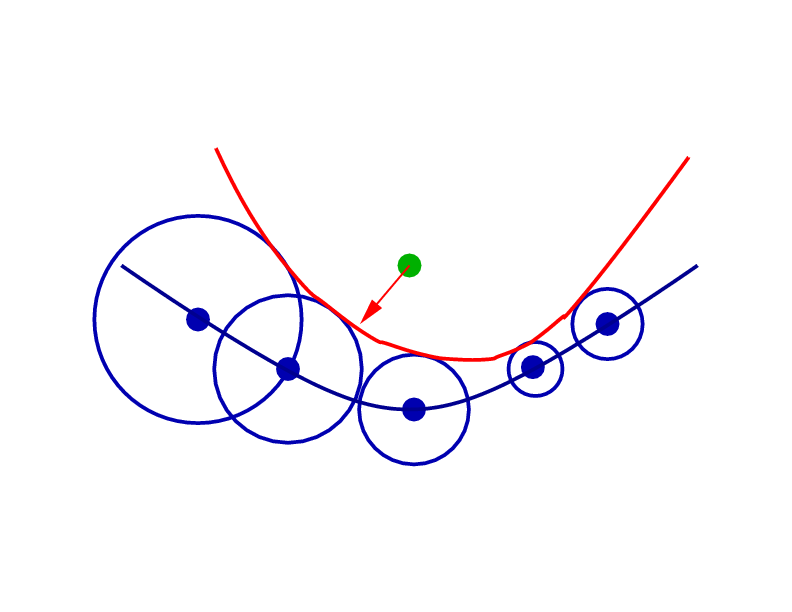
    Isotropic: Expanding waves are always circular, even if they are different sizes. Anisotropic: Expanding waves are strangely shaped: information doesn't always arrive along trajectory perpendicular to evolving front.


    The Way Out: Ordered Upwind Methods

    The way out of this, that is, the way to keep the idea of Dijkstra's method and a one-pass algorithm is to keep track of the ratio between the fastest and slowest speed at each point. This anisotropy ratio reveals something important: although the information may not come along a trajectory perpendicular to the front, it can't come from very far away. In the figure below, the only trajectories on the front that can send information to the green spot are those that start no further than the anisotropy ratio times the distance to the closest point.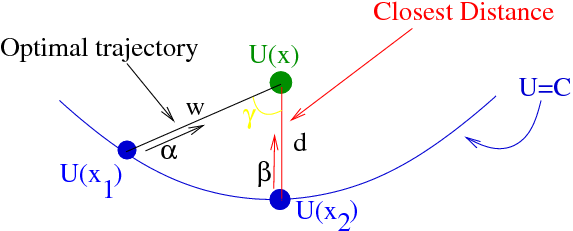
    This means that one can keep the entire Dijkstra-like one-pass metholodogy, only now it can be extended to anisotropic speeds. These methods are called Ordered Upwind Methods, because they maintain an ordering of the points and systematically compute the solution by relying on known, previously computed information which lies upstream.

    Results

    Below are four examples computed using this technique. Four layers with wavy sinusoidal boundaries are considered: each has an elliptical speed profile, each oriented differently, in which there is an anisotropic preferred speed of propagation. A wave is started at the center point: you can see that the equiarrival curves are significantly contorted as the anisotropic effects determine the wave's propagation.


    Details

    Ordered Upwind Methods are a class of Dijkstra-like schemes to approximate the solution of convex static Hamilton-Jacobi equations. They are of order N log N, where N is the number of points in the computational domain, and both semi-Lagrangian and fully Eulerian versions have been developed. Numerical solutions to these problems are typically obtained by solving a large system of coupled non-linear discretized equations. In contrast, Ordered Upwind Methods, use partial information about the characteristic directions, obtained by examining the anisotropy ratio between fastest and slowest speeds to de-couple the non-linear systems, producing one-pass algorithms of greatly reduced computational labor.

    References

    • Ordered Upwind Methods for Static Hamilton-Jacobi Equations, ,
            Sethian, J.A., and Vladimirsky, A., Proceedings of the National Academy of Sciences, 98, 11069-11074, 2001.
      This paper List of downloadable publications


    • Ordered Upwind Methods for Static Hamilton-Jacobi Equations: Theory and Algorithms, ,
            Sethian, J.A., and Vladimirsky, A., SIAM J. Numer. Anal., 41, 1, pp. 325-363, 2003
      This paper List of downloadable publications


    • Ordered Upwinds Methods for Hybrid Control, ,
            Sethian, J.A., and Vladimirsky, A., Proceedings Fifth International Conference on Hybrid Systems and Control, Ed. C. Tomlin and M.R. Greenstreet, LCNS 2289, Springer, pp. 393, 2002
      This paper List of downloadable publications