HOME

OVERVIEW

APPLICATIONS

Soap Bubbles

Medical Imaging

Chemical Pathways

INTERACTIVE APPLETS

HISTORY OF THE METHODS/FLOW CHART

PUBLICATIONS

EDUCATIONAL MATERIAL

ACKNOWLEDGEMENTS

ABOUT THE AUTHOR/CV

Copyright:
1996-2010
J.A. Sethian

Molecular Pathways in Chemical Systems

Overview
The passage of a molecule through the labyrinth of a chemical system is critical to catalysis, gas separation such as carbon sequestration, and other important chemical processes. Access to a particular sites where reactions can occur is critical, and such sites are often buried in pockets or hidden cavities. The accessible volume of a chemical system is important in determining a system's physical properties, such as diffusion, viscosity, and electrical conductivity. Computer simulations using molecular dynamics are often used to model potential molecule/labyrinth interactions, however, such simulations are time-consuming, often relying on complex molecular dynamics simulations.

Here are some questions to anwer:

Can a given molecule pass chemical system?
Volume accessible to a given molecule
Molecular transport pathways (the shortest path, the most efficient path)

Answering these questions is valuable in many applications, including analyzing porous materials, such as zeolites, metal-organic frameworks, understanding catalysis (e.g. oil refinement), and gas separation (CO2 sequestration). Another application is in understanding proteins, where one wants to determine the accessibility of a molecule to an active site of an enzyme.

An Example Question
Can a molecule traverse into a buried pocket? This question is hard to answer, even using simplified model that ignores physical interactions and dynamical effects. One current technique is to approximate the molecule as a spherical problem, or as a rigid structure. However, it is easy to see that that this might miss a lots of possible ways to snake through a complex structure. For example: look at the drawing below:

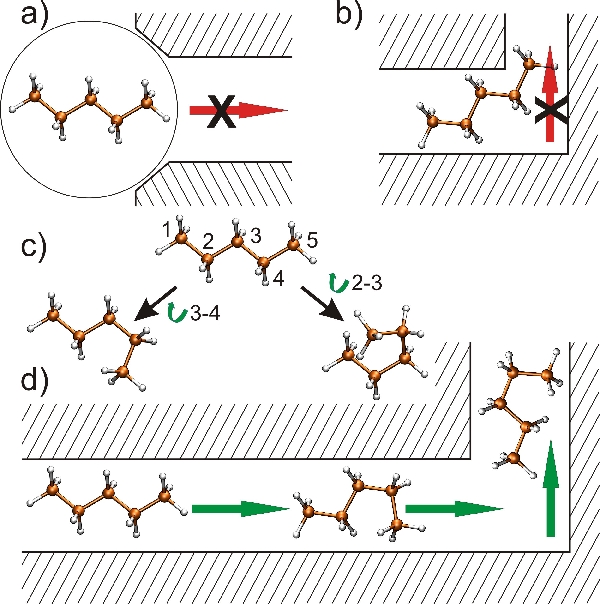
In (a), we try representing a molecule by the smallest sphere that contains it: it is easy to see that this spherical approximation overestimates the actual size of the molecule, and the spherical version is too big to even squeeze into the entrance.

In (b), we try to go one step better, and use the actual molecule, but we don't let it bend and twist. Because of this, it cannot make its way around a tight corner, and gets stuck.

In (c), we instead model a molecule as having two internal degrees of freedom corresponding to rotations along the bonds connecting atoms 2-3 and 3-4. Because we allow this more versatile model, the newly defined flexible molecule can trespass the structure and change its shape if required to maneuver in tight corners.

Fast Marching Methods in High Dimensional Configuration Space for Flexible Molecular Worms
Using partial differential equations (PDE)-based path planning robotic algorithms, one can perform a sort of mathematical triage, by testing whether a molecular worm made of blocks together with flexible links, can pass through a chemical labyrinth. The key is the use of high dimensional Fast Marching Method connected to robotic navigation to quickly compute possible paths through a complex structure. Here, the interface grows to explore the space of accessible volume where a probe might be able to reach. Here, three dimensional physical space is combined with a high dimensional rotational space, corresponding to the possible rotations and twists of each of the molecular arms. This high dimensional space is called "configuration space", and we call the moving object a "molecular worm".

We are trying to test to see if this molecular worm can wiggle its way through the chemical labyrinth. We can check this by using the Fast Marching Method in six dimensional space. For more complex molecules, this can lead to a giant problem in very high dimensional configuration space, and needs significant computational resources to solve PDE in high dimensional configuration space

Sample Application
As a sample application, we find the shortest path of butane across one unit cell of periodic structure of MFI zeolite, which is a microporous mineral material. Our model assumes that butane has one internal degree of freedom (l = 1) dihedral angle, which leads to a seven dimensional Fast Marching Method. We take .02nm steps for the real space grid, which gives 100x100x67 grid points. We sample the molecular orientation every 45 degrees, and the internal degree of freedom is sampled every 90 degrees.

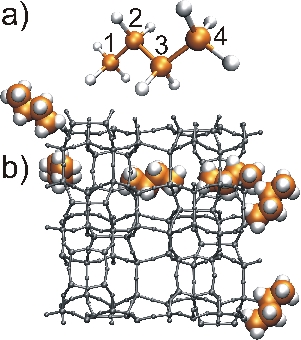
In figure (a), we show the butane molecule and atom numbering. In Fig (b), we show the shortest path across one unit cell of periodic MFI zeolite structure. Larger radii of butane's atoms were used to improve clarity of the figure.

Details
The calculations were made using a Fast Marching Method in six dimensional space. We solve the Eikonal equation using a speed function synthesized from testing all configurations against the wall, and then start a probe exterior to the structure, solving until all accessible spots are reached. Flexible, rubber-like walls are modeled using a modified speed function to mimic additional energy required to push against boundaries.
References
Haranczyk, M. and Sethian, J.A., Navigating Molecular Worms Inside Chemical Labyrinths, Proceedings of the National Academy of Sciences, 106, pp. 21472-21477, 2009. List of downloadable publications