HOME

OVERVIEW

APPLICATIONS

  • Geometry
  • Soap Bubbles
  • Medical Imaging
  • Robotics
  • Fluids
  • Semiconductors
  • Wave Propagation
  • Image Denoising
  • Optimal Design
  • Seismic Analysis
  • Tumor Modeling
  • Optimal Control
  • InkJet Plotters
  • Traveling Salesmen
  • ViscoElastic Flow
  • Pinching Droplets
  • Chemical Pathways

    INTERACTIVE APPLETS

    HISTORY OF THE METHODS/FLOW CHART

    PUBLICATIONS

    EDUCATIONAL MATERIAL

    ACKNOWLEDGEMENTS

    ABOUT THE AUTHOR/CV








    Copyright:
    1996-2010
    J.A. Sethian

    • Robotic Navigation

    Overview

    Suppose you live in an apartment with lots of corridors and long skinny halls. And, you've finally scraped up the money to buy a piano, which you need to get from the front door to the back room. The first question is, is it actually possible to twist and turn the piano in such a way as to get it back there? And second, if it is, what is the shortest path?

    This is a problem in robotic navigation with constraints; the navigation part is to find the shortest path; the constraint part is the requirement that you don't accidentally add a few new holes in the walls as you move the piano. Fast Marching Methods provide a very quick way to solve this problem.

    Finding the Shortest Path

    An easy version

    As a warm-up, suppose you are standing in a giant parking lot. You are at point A, your car is at point B, and there are no other cars in the lot. If you want the shortest path to your car, just draw the straight line shown in the figure on the left.
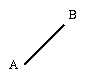
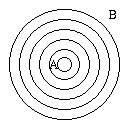
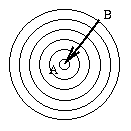
    Straight line from A to B Expanding front around A Trace back to find path
    But there's a different way to find this path. Imagine a front expanding from point A in all directions. Since it doesn't "cost" you any more to walk in one direction over another, let the front expand with speed 1 in all directions. That means that the expanding front will be a growing circle around point A, which will eventually touch point B. Once the front touches point B, you can find the shortest path by starting at point B and proceeding backwards along the path that is always perpendicular to the expanding front. If you do this, you'll get the straight line shown in the figure on the right.

    A slightly harder version

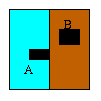
    Now, let's imagine that one half of the parking lot is full of snow, and it's slower to walk through snow. Furthermore, you're standing on the snowy side, and your car is on the dry side. In this case, the "shortest" path (that is, the one that takes the least time), as shown in the figure on the left, is not always a straight line. But we can still use our front propagation technique: we expand a front around point A, only this time the front expands faster when it is on dry pavement than it does over the snow. Once the front hits the car, we again trace backwards from B to A, always going perpendicular to the front, and construct the shortest path!
    Left=snow, Right=dry Expand front around A Trace back to find path

    An even harder version

    Now, let's add other cars to the lot. We can represent those cars as places where the "cost" of traveling is infinity: it takes forever to walk through a car. Again, we solve our front propagation problem, trace back, and construct the optimal path.
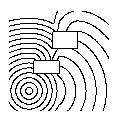
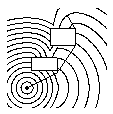
    Snow + Dry + Other Cars Expand front around A Trace back to find path

    By the way, you were carrying a ladder

    Yup, and the ladder can't be tilted on its side, and the cars are really big so that you can't pick the ladder over the cars. That means that you are no longer a point, but now have to negotiate the ladder through the narrow paths between cars. It's the same thing; we propagate a front outwards from A to B, adjusting the speed corresponding to our ability to walk or turn the ladder at any point, and then, when it reaches B, we can trace backwards to find the fastest path.

    Finding the Shortest Path

    The equation that describes the arrival time of this expanding front as it depends on the possible speed at any point and direction is the Eikonal equation. The Fast Marching Method is used to solve the equation for the first arrival time, and then we can trace backwards from B to A to construct the actual path.

    (51K) (71K)
    Movies of Moving a Piano in a San Francisco Apartment


    An Interactive Java Applet:

    Design your own obstacle course and robot, and then let the Fast Marching Method compute the optimal path





    Details

    The calculations were made using a Fast Marching Method to solve the Eikonal equation given by | grad T | = f(x,y,theta) for first arrival times, coupled to back propagation using Heun's method for the O.D.E. u= grad T given by the gradient field. The Eikonal equation in configuration space is obtained by discretizing the domain in x and y, as well as the rotational angle theta. The constraints of the walls are manifested by modifying configuration space as a function of the angle of the stick relative to the domain geometry. Thus, the full problem is a three-dimensional configuration space, and the back propagation trajectory through configuration space is then shown in the movie at each time step. Additional movies



    References

    • Fast Marching Methods for Robotic Navigation with Constraints : Kimmel, R., and Sethian, J.A., CPAM Report 669, Univ. of California, Berkeley, 1996. Download publications