HOME

OVERVIEW

APPLICATIONS

  • Geometry
  • Soap Bubbles
  • Medical Imaging
  • Robotics
  • Fluids
  • Semiconductors
  • Wave Propagation
  • Image Denoising
  • Optimal Design
  • Seismic Analysis
  • Tumor Modeling
  • Optimal Control
  • InkJet Plotters
  • Traveling Salesmen
  • ViscoElastic Flow
  • Pinching Droplets
  • Chemical Pathways

    INTERACTIVE APPLETS

    HISTORY OF THE METHODS/FLOW CHART

    PUBLICATIONS

    EDUCATIONAL MATERIAL

    ACKNOWLEDGEMENTS

    ABOUT THE AUTHOR/CV








    Copyright:
    1996-2010
    J.A. Sethian

    • Continuous Traveling Salesmen Problem

    Everybody knows the Traveling Salesmen problem, even if they have never heard it formally posed: given a collection of cities, and a cost of traveling from one city to the next, find a way to travel to all the cities with the minimal total cost. The Traveling Salesmen Problem (TSP) is typically posed as follows: you are given a set of cities and a collection of links between the cities: each link carries a cost of traveling between the two cities (this is the symmetric TSP problem: if the cost in going in both directions is not the same, then the problem is asymmetric).
    Is the optimal path A to B to C to D to E, or is it A to B to D to E to C?


    The problem has been the subject of centuries of study: it is difficult to find the optimal solution once the number of cities gets beyon a few dozen. Consequently, many heuristic algorithms have been posed which surrender trying to find the optimal solution in exchange for finding efficient algorithms to find very good solutions. The trade is usually worth it: spending 1000 hours of computer time to find the exact solution to a problem with 100 cities doesn't seem worth it compared to finding a very good solution to a problem with 10000 cities in a few minutes.

    Continuous Traveling Salesmen Problem

    We are interested in a different version of this problem. Suppose the cost of traveling between the cities themselves is not known? Imagine that there are obstacles in the domain, or that the cost of traveling from one point to the next depends on position. In the figure below, if the cost of traveling through different colored regions is different, then you don't even know the path from one city to the next, let alone how to travel through all of them.
    The darker the area, the higher the cost. What is the cheapest path that visits all points?


    We can in fact solve this problem by embedding the Fast Marching Method inside an algorithm to solve the Traveling Salesmen Problem. There are two approaches:
    1. Pick a city, and run the Fast Marching Method to compute the shortest path from every other city back to the city. Do this for each city. Now that you have all the costs and paths between all pairs of cities, pass the graph and its weights to any Traveling Salesmen Problem.
    2. The above is wasteful: perhaps you really don't need to compute all the paths, since many won't be taken. A better idea is to embed the Fast Marching Method into the TSP algorithm itself.


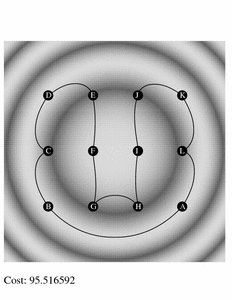
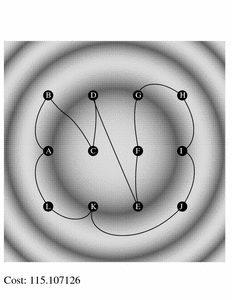
    Below, we show the results of doing exactly this. We embed the Fast Marching Method inside two different algorithms:
    • The first is an optimal algorithm that builds and all partial paths, running the Fast Marching Method on the fly, and terminates as soon as a complete path is formed.
    • The second couples to the Fast Marching Method to Christofides algorithm for computing a non-optimal but, nonetheless, very good solution.
    Optimal Solution: Total Cost=95.5 Heuristic Solution: Total Cost=115.1
    Paths to Visit all Cities: Darker the Region, the Higher the Cost


    An Interactive Java Applet:

    Distribute some cities, pick a cost function, and find the cheapest path.




    Details:
    We consider a problem in which we are given a domain, a cost function which depends on position at each point in the domain, and a finite collection of points in the domain. The goal is to determine the cheapest closed path that visits each point in the domain once. This can be thought of as version of the Traveling Salesman Problem, in which an underlying known metric determines the cost of moving through each point of the domain, but in which the actual shortest path between cities is unknown at the outset. We describe algorithms for both a heuristic and an optimal solution to this problem. The runtime of the optimal algorithm is exponential, as expected, and the order of the heuristic algorithm is at worst case M*N log N, where M is the number of cities, and $N$ the size of the computational mesh used to approximate the solutions to the shortest paths problems. The average runtime of the heuristic algorithm is linear in both number of cities and size of the mesh.

    References
    • Fast Marching Methods for the Continuous Traveling Salesman Problems,
            Andrews, J., and Sethian, J.A., to appear, Proceedings National Academy Sciences, 2006.
      PDF       Topic area: Optimal Control