HOME

OVERVIEW

APPLICATIONS

  • Geometry
  • Soap Bubbles
  • Medical Imaging
  • Robotics
  • Fluids
  • Semiconductors
  • Wave Propagation
  • Image Denoising
  • Optimal Design
  • Seismic Analysis
  • Tumor Modeling
  • Optimal Control
  • InkJet Plotters
  • Traveling Salesmen
  • ViscoElastic Flow
  • Pinching Droplets
  • Chemical Pathways

    INTERACTIVE APPLETS

    HISTORY OF THE METHODS/FLOW CHART

    PUBLICATIONS

    EDUCATIONAL MATERIAL

    ACKNOWLEDGEMENTS

    ABOUT THE AUTHOR/CV








    Copyright:
    1996-2010
    J.A. Sethian

    • Visco-Elastic Flow

    Visco-elastic flow is a remarkably interesting subject. Water, for example, has a viscosity that is independent of the strain that you put on it. In contrast, Non-Newtonian flows have a vicosity that changes with the strain rate. I can't do better than Wikipedia:

    "An inexpensive, non-toxic sample of a non-Newtonian fluid can be made quite easily by adding corn starch to a cup of water. Add the starch in small portions and stir in slowly. When the suspension nears the critical concentration - becoming like single cream in consistency - the so called "shear thickening" property of this non-Newtonian fluid becomes apparent. The application of force - for example by stabbing the surface with a finger, or rapidly inverting the container holding it - leads to the fluid behaving like a solid rather than a liquid. More gentle treatment, such as slowly inserting a spoon, will leave it in its liquid state.Trying to jerk the spoon back out again, however, will trigger the return on the temporary solid state."


    Applications involving viscoelastic fluid jets are quite broad, and include such areas as microdispensing of bioactive fluids through high throughput injection devices, creation of cell attachment sites, scaffolds for tissue engineering, coatings and drug delivery systems for controlled drug release, and viscoelastic blood flow flow past valves.

    Building visco-elastic flows using level set methods to track the interface is quite a challenge. Tracking the interface is not too difficult, and solving the fluid equations for two fluids can be done using an embedded level set method coupled to a projection scheme for incompressible flow. The challenge comes in dealing with something called the "high Weissenberg" problem: when the effects of visco-elastic flow become large, numerical schemes tend to go unstable and have trouble converging.

    Below, we show the results of a coupled level set/projection method scheme to compute visco-elastic flows in the context of ink jet plotters. Regular dye-based inks used in desktop printers are Newtonian, which means the relation between the stress tensor and the rate of deformation tensor at an instant is linear and not related to any other instant. The use of pigment-based inks at the end of the 1990's improved the color durability of a ink jet printout, however, pigment-based inks and inks used in industrial printing applications are usually viscoelastic. And there starts the problem.

    In the figures below, we imagine two fluids, similar to our ink jet simulation. The "ink" is taken as visco-elastic, while the air is a pure Newtonian fluid. As you see in the movies below, as we turn up the "visco-elastic" part of the equations as the figures move from right to left, the ejected bubble has a harder and harder time escaping, until, ultimately, the visco-elastic effects cause the jet to tract to its base.

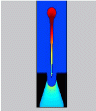
    Axisymmetric (3D) Ejection of Viscoelastic Ink
    Pure A little More Even more
    Newtonian Flow viscoelasticity viscoelasticity viscoelasticity



    Details

    We developed a coupled finite difference algorithm on rectangular grids for viscoelastic ink ejection simulations. The ink is modeled by the Oldroyd-B viscoelastic fluid model. The coupled algorithm seamlessly incorporates several things: (1) a coupled level set-projection method for incompressible immiscible two-phase fluid flows; (2) a higher-order Godunov type algorithm for the convection terms in the momentum and level set equations; (3) a simple first-order upwind algorithm for the convection term in the viscoelastic stress equations; (4) central difference approximations for viscosity, surface tension, and upper-convected derivative terms; and (5) an equivalent circuit model to calculate the inflow pressure (or flow rate) from dynamic voltage.

    References