Level Set Methods: An initial value formulation

Tracking a moving boundary

Suppose you are given an interface separating one region from another, and a speed F that tells you how to move each point of the interface. In the figure below, a black curve separates a dark blue inside from a light blue outside, and at each point of the black curve the speed F is given. This speed can depend on a variety of physical effects. For example

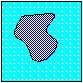
Imagine that the dark blue is ice and the light blue is water. Then the boundary can shrink as the ice melts, or grow as the ice freezes; the speed then depends on the temperature jump between the two.
Imagine that the dark blue is honey and the light blue is tea. Then the boundary moves as the heavy fluid falls into to the light one, and the speed depends on gravity, the ratio of the fluid densities, and the surface tension between the two.

Most numerical techniques rely on markers, which try to track the motion of the boundary by breaking it up into buoys that are connected by pieces of rope. The idea is to move each buoy under the speed F, and rely on the connecting ropes to keep things straight. The hope is that more buoys will make the answer more accurate.

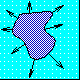
Unfortunately, things get pretty dicey if the buoys try to cross over themselves, or if the shape tries to break into two; in these cases, it is very hard to keep the connecting ropes organized. In three dimensions, following a surface like a breaking ocean wave is particular tough.

The level set approach

Rather than follow the interface itself, the level set approach introduced by Osher and Sethian instead takes the original curve (the red one on the left below), and builds it into a surface. That cone-shaped surface, which is shown in blue-green on the right below, has a great property; it intersects the xy plane exactly where the curve sits. The blue-green surface on the right below is called the level set function, because it accepts as input any point in the plane and hands back its height as output. The red front is called the zero level set, because it is the collection of all points that are at height zero.

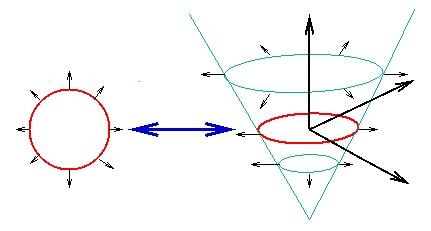
The original front					The level set function
Front lies in xy plane					Front is intersection of Surface and xy plane

Another way to see why this is called a "level set surface" is to imagine a saw that can cut a slice of the surface and then drop it onto the xy plane. However, the slice has to be perfectly level.

If the saw cuts the blue-green level set surface at height zero above the xy plane, the ring that will drop to the xy plane will be the original red front.
If the saw cuts at some other height, a different ring will drop down, producing one of the blue-green curves instead.

How do you move the front?

The idea is that instead of moving the red front, which can do all sorts of weird things, one might try and instead move the surface on the right. In other words, the level set function expands, rises, falls, and does all the work. To find out where the front is, get out the saw and cut the surface at zero height.

(290K)

Red curve is zero level set

Why is this called an "initial value formulation"?

The reason it is called an "initial value formulation" is because the initial position of the interface gives initial data for a time-dependent problem. In other words, the solution starts at a given position and evolves in time.

Why is this a good idea?

So far, it might seem crazy to take the problem of a moving curve and trade it in for a moving surface. The reason this is a good idea lies in taking a good look at the surface on the right. It will always be "nice"; the red front can get wildly contorted, but our blue level set function is well-behaved. All the complicated problems of breaking and merging are easily handled. Better yet, everything works for three dimensional surfaces with no change..

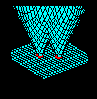(260K)

Initial front is two curves that join together as they grow

An equally important advantage is that it is easy to build accurate numerical schemes to approximate the equations of motion. That's because rather than track buoys around, which might end up colliding, one can instead stand on the xy plane and compute the answer. Using terminology from a completely different language, marker particle methods are man-to-man coverage, while level set methods are a zone defense. All together, the trick of embedding the front in a higher dimensional function is well worth the added cost (in fact, with some work, that cost be made the same as that of marker techniques).

What is the difference between Fast Marching Methods and Level Set Methods?

Fast Marching Methods are designed for problems in which the speed function never changes sign, so that the front is always moving forward or backward. This allows us to convert the problem to a stationary formulation, because the front crosses each red grid point only once. This conversion to a stationary formulation, plus a whole bunch of numerical tricks, gives it its tremendous speed

Level Set Methods are designed for problems in which the speed function can be positive in some places are negative in others, so that the front can move forwards in some places and backwards in others. While significantly slower than Fast Marching Methods, embedding the problem in one higher dimension gives the method tremendous generality.

Details

Level set methods

The Osher-Sethian level set method tracks the motion of an interface by embedding the interface as the zero level set of the signed distance function. The motion of the interface is matched with the zero level set of the level set function, and the resulting initial value partial differential equation for the evolution of the level set function resembles a Hamilton-Jacobi equation. In this setting, curvatures and normals may be easily evaluated, topological changes occur in a natural manner, and the technique extends trivially to three dimensions. This equation is solved using entropy-satisfying schemes borrowed from the numerical solution of hyperbolic conservation laws which produce the correct viscosity solution. For details, see the technical explanations and flow chart.

References:

An Analysis of Flame Propagation, Sethian, J.A., Ph.D. Dissertation, Dept. of Mathematics, University of California, Berkeley, CA, 1982. List of downloadable publications
Curvature and the Evolution of Fronts, Sethian, J.A., Comm. in Math. Phys., 101, pp. 487--499, 1985. This paper List of downloadable publications

Numerical Methods for Propagating Fronts, Sethian, J.A., in Variational Methods for Free Surface Interfaces, Proceedings of the Sept, 1985 Vallambrosa Conference, Eds. P. Concus and R. Finn, Springer-Verlag, NY, 1987. This paper List of downloadable publications

Fronts Propagating with Curvature-Dependent Speed: Algorithms Based on Hamilton--Jacobi Formulations, Osher, S., and Sethian, J.A., Journal of Computational Physics, 79, pp. 12--49, 1988. This paper List of downloadable publications