HOME

OVERVIEW

APPLICATIONS

  • Geometry
  • Soap Bubbles
  • Medical Imaging
  • Robotics
  • Fluids
  • Semiconductors
  • Wave Propagation
  • Image Denoising
  • Optimal Design
  • Seismic Analysis
  • Tumor Modeling
  • Optimal Control
  • InkJet Plotters
  • Traveling Salesmen
  • ViscoElastic Flow
  • Pinching Droplets
  • Chemical Pathways

    INTERACTIVE APPLETS

    HISTORY OF THE METHODS/FLOW CHART

    PUBLICATIONS

    EDUCATIONAL MATERIAL

    ACKNOWLEDGEMENTS

    ABOUT THE AUTHOR/CV








    Copyright:
    1996-2010
    J.A. Sethian

    • Minimal Surfaces and Soap Bubbles

    Overview

    Take a piece of wire, connect the two ends together, and dip it in a bath of soapy water. The thin membrane that spans the wire boundary is a minimal surface; of all possible surfaces that span the boundary, it is the one with minimal energy. One way to think of this "minimal energy; is that to imagine the surface as an elastic rubber membrane: the minimal shape is the one that in which the rubber membrane is the most relaxed. For example, a minimal surface that spans two rings is given by the catenoid surface below:





    Notice that this is not the only possible minimal surface: another one consists of the two disks; one spanning each ring. This means minimal surfaces exist locally ; each one only has to be most relaxed membrane of all the ones close by.


    Level Set Methods for Minimal Surfaces

    Given a wire frame, how can one find a minimal surface that spans the frame. Motion under curvature provides an appealing way to find the surface.

    To illustrate the idea, what is the "minimal" curve connecting two points? Although its obvious that the straight line connecting the two points is the minimal curve, a different way to construct the minimal surfaces begins with any curve at all connecting the two points.

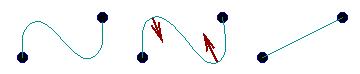
    Any curve Curvature flow Minimal curve

    If this initial curve moves according to its curvature , and is forced to stay attached to the endpoints, then the kinks will disappear and the curve will straighten itself out.

    A level set perspective can be used to find such a minimal surface. Start with any membrane at all that spans the wire frame, and then let that surface evolve under curvature flow . As long as it stays attached to the frame, it will become a minimal surface when it is through moving. Because the level set approach allows a surface to break and move as it evolves, this approach can find minimal surfaces that are very different from the initial shape. For example, if the two rings in the above example are pulled slightly apart, the only minimal surface is the two disks:
    Evolution of Catenoid Splitting into two disks



    Movies

    Initial Rings Close Together: Initial Rings Farther Apart
    (Movie: not yet constructed) (Movie: not yet constructed)




    Details

    The calculations were made using a level set method to track the motion of evolving surface. An initial surface is attached to the wire frame, and then embedded as the zero level set of the signed distance function in all of space. This level set function is evolved under mean curvature, with boundary conditions enforced to always attach the front to the boundary. The level set function is periodically re-initialized to maintain uniformity in its spacing. The final state of the calculation is the minimal surface.

    References

    Chopp, D.L., Computing Minimal Surfaces via Level Set Curvature Flow , Jour. of Comp. Phys., Vol. 106, pp. 77--91, 1993.
    List of downloadable publications