
Low-dimensional
manifold and
high-dimensional categories
A conference in honor of
Michael Hartley Freedman
June 6-10, 2011
UC Berkeley
video
Printable PDF version of Abstracts
| Speaker: Yakov
Eliashberg Title: Flexible and rigid Weinstein manifolds The symplectic homology ring is a very efficient tool in distinguishing affine (Weinstein) symplectic manifolds. On the other hand, if symplectic homology is trivial the distinction is difficult. Though there are known some examples of non-symplectomorphic Weinstein manifolds with trivial symplectic homology, is not at all clear how much symplectic life exists beyond symplectic homology. The result discussed in the talk indicates that not much if dimension 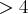 .
It turns out that a typical operation which kills symplectic homology
transforms a Weinstein manifold into a pure topological object which
abides a certain .
It turns out that a typical operation which kills symplectic homology
transforms a Weinstein manifold into a pure topological object which
abides a certain 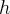 -principle. A key ingredient in the
proof is a recent result of my student Max Murphy who proved a
surprising -principle. A key ingredient in the
proof is a recent result of my student Max Murphy who proved a
surprising 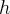 -principle for Legendrian knots in
contact manifolds of dimension -principle for Legendrian knots in
contact manifolds of dimension 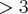 . . Parts of this work are joint with K. Cieliebak and F. Bourgeois-T. Ekholm. |
| Speaker: Ron
Fintushel Title: Smooth 4-manifolds: 2011 (Slides) This will be an expository lecture on the state of affairs with regard to smooth structures on simply connected 4-manifolds with 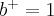 . There has been considerable progress
on this front in the last 5 to 10 years. I will concentrate on
techniques and ideas involved in making this progress and survey the
results that these techniques give as well as open questions and
conjectures. . There has been considerable progress
on this front in the last 5 to 10 years. I will concentrate on
techniques and ideas involved in making this progress and survey the
results that these techniques give as well as open questions and
conjectures. |
| Speaker: David Gay Title: Low-dimensional Morse 2-functions A Morse 2-function is just a generic (stable) smooth map from a smooth n-manifold to a 2-manifold; here we will focus on maps to 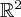 . We will look at some basic examples
when the domain
is 2-dimensional, just to get our intuition on the right track, and
then look at the case where the domain is 3- or 4-dimensional. I will
state some results that are the result of joint work with Rob Kirby
and stress the underlying connection with Cerf theory (the study of
generic homotopies between ordinary Morse functions). . We will look at some basic examples
when the domain
is 2-dimensional, just to get our intuition on the right track, and
then look at the case where the domain is 3- or 4-dimensional. I will
state some results that are the result of joint work with Rob Kirby
and stress the underlying connection with Cerf theory (the study of
generic homotopies between ordinary Morse functions). |
| Speaker: Cameron
Gordon Title: Exceptional Dehn filling It is rare for a hyperbolic knot in 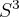 to have a non-trivial Dehn surgery
that yields a non-hyperbolic 3-manifold, but it does happen. More
generally, it is rare for a hyperbolic 3-manifold to have a non-trivial Dehn surgery
that yields a non-hyperbolic 3-manifold, but it does happen. More
generally, it is rare for a hyperbolic 3-manifold 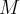 to
have two non-hyperbolic Dehn fillings to
have two non-hyperbolic Dehn fillings 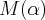 and and 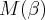 along a given cusp. Consequently, one
wonders if it might be possible to describe all such exceptional
triples along a given cusp. Consequently, one
wonders if it might be possible to describe all such exceptional
triples 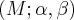 . We will give a survey of progress
towards this goal, and some of the problems that remain. . We will give a survey of progress
towards this goal, and some of the problems that remain. |
| Speaker: Sergei Gukov Title: The homological algebra of knots and BPS states A physical interpretation of knot homologies as spaces of the so-called "refined BPS states" leads to many interesting and often surprising predictions, ranging from concrete expressions for homological knot invariants associated with higher representations of SL, SO, and Sp classical groups to intricate webs of spectral sequences and anti-commuting differentials acting on the triply-graded theories categorifying the HOMFLY and Kauffman polynomials. In this talk, I will review the enterprise of this connection between (enumerative) geometry and knot theory and, if time permits, describe some of the latest developments, related to the interpretation of spectral sequences and differentials, and wall crossing for refined / motivic BPS invariants. |
| Speaker: Ko Honda Title: HF=ECH via open book decompositions (Slides) The goal of this talk is to sketch a proof of the equivalence of Heegaard Floer homology (due to Ozsvath-Szabo) and embedded contact homology (due to Hutchings). This is joint work with Vincent Colin and Paolo Ghiggini. |
| Speaker: Michael
Hutchings Title: Applications of embedded contact homology (Slides) Embedded contact homology is an invariant of contact three-manifolds which is isomorphic to versions of Heegaard Floer homology and Seiberg-Witten Floer homology. I will give an introduction to what ECH is good for, aside from being isomorphic to other Floer theories. For example, the detailed structure of ECH leads to extensions of the Weinstein conjecture (joint work with Cliff Taubes). In addition, maps on ECH induced by four-dimensional symplectic cobordisms lead to a proof of the Arnold chord conjecture in three dimensions (joint with Taubes), and to new symplectic embedding obstructions in four dimensions which are sharp in some cases. |
| Speaker: Slava
Krushkal Title: The A-B slice problem (Slides) In his groundbreaking 1982 paper Michael Freedman proved a disk embedding theorem, leading to a classification of simply-connected topological 4-manifolds. Although the class of fundamental groups for which such geometric classification techniques work has since been extended, the central case of free groups remains open. The A-B slice problem is a reformulation (due to Freedman) of this question in terms of a generalized link-slicing problem. This talk will discuss the history of the problem, as well as recent developments and ideas for a solution. |
| Speaker: Yanki Lekili Title: Fukaya category of the punctured torus In joint work with Tim Perutz, we give a complete characterization of the Fukaya category of the punctured torus, denoted by 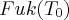 . This, in particular, means that one
can write down an explicit minimal model for . This, in particular, means that one
can write down an explicit minimal model for 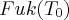 in the form of an in the form of an 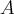 -infinity
algebra, denoted by -infinity
algebra, denoted by 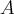 , and classify , and classify 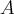 -infinity
structures on the relevant algebra. A result that we will discuss is
that no associative algebra is quasi-equivalent to the model -infinity
structures on the relevant algebra. A result that we will discuss is
that no associative algebra is quasi-equivalent to the model 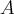 of
the Fukaya category of the punctured torus, i.e., of
the Fukaya category of the punctured torus, i.e., 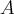 is
non-formal. is
non-formal. 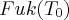 will be connected to many topics of
interest: will be connected to many topics of
interest: 1) It is the boundary category that we associate to a 3-manifold with torus boundary in our extension of Heegaard Floer theory to manifolds with boundary, 2) It is quasi-equivalent to the category of perfect complexes on an irreducible rational curve with a double point, an instance of homological mirror symmetry. |
| Speaker: Scott
Morrison Title: Khovanov homology for 4-manifolds. I'll describe an invariant of smooth 4-manifolds defined in terms of Khovanov homology. It associates a doubly-graded vector space to each 4-manifold (optionally with a link in its boundary), generalizing the Khovanov homology of a link in the boundary of the standard 4-ball. For now, we can only make the construction in characteristic two. I'll finish by talking about relations to TQFT, and the prospects for concrete calculations. This is joint work with Chris Douglas and Kevin Walker. |
| Speaker: Frank Quinn Title: Topology in the mystery dimension Overview of 4-dimensional topology, with historical notes. |
| Speaker: Martin
Scharlemann Title: Fibered knots and potential counterexamples to the Property 2R and Slice-Ribbon Conjectures (Slides) If there are any two component counterexamples to the Generalized Property R Conjecture, a least genus component of all such counterexamples cannot be a fibered knot. Furthermore, the monodromy of a fibered component of any such counterexample has unexpected restrictions. The simplest plausible counterexample to the Generalized Property R Conjecture could be a two component link containing the square knot. We characterize all two-component links that contain the square knot and which surger to 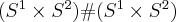 . We exhibit a family of such links
that are probably counterexamples to Generalized Property R. These
links can be used to generate slice knots that do not seem to be
ribbon. . We exhibit a family of such links
that are probably counterexamples to Generalized Property R. These
links can be used to generate slice knots that do not seem to be
ribbon. |
| Speaker: Rob
Schneiderman Title: Higher-order intersections in low-dimensional topology (Slides) The failure of the Whitney move in dimension 4 can be measured by constructing higher-order intersection invariants of Whitney towers built from iterated Whitney disks on immersed surfaces in 4--manifolds. For Whitney towers on immersed disks in the 4--ball, some of these invariants can be identified with previously known link invariants like Milnor, Sato-Levine and Arf invariants. This approach also leads to the definition of higher-order Sato-Levine and Arf invariants which detect the obstructions to framing a twisted Whitney tower, and appear to be new invariants. Recent joint work with Jim Conant and Peter Teichner has shown that, together with Milnor invariants, these higher-order invariants classify the existence of (twisted) Whitney towers of increasing order in the 4--ball. |
| Speaker: Catharina
Stroppel Title: Fractional Euler characteristics and completed Grothendieck groups Khovanov homology is a categorification of the Jones polynomial. The fact that the Jones polynomial can be normalized such that it is defined over the integers is used hereby in a crucial way here. When constructing the colored Jones polynomial and Reshetikhin-Turaev 3-manifold invariants naturally polynomials over rational numbers or rational functions in a variable q occur. In this talk I want to address the problem of categorifying such functions. The main idea here is a p-adic completion of the Grothendieck groups and the notion of mixed categories with weight filtrations. I will illustrate the concept by categorified link invariants and 3j-symbols. |
| Speaker: Peter
Teichner Title: Higher categories for low-dimensional topologists We'll motivate the definition of d-categories via the d-dimensional bordism category of manifolds (with geometric structures). Then we'll go through the low-dimensional cases d=0,1 and 2 and rediscover some well known notions With the addition of one odd direction, the spaces of super symmetric Euclidean field theories (aka representations of the super Euclidean bordism category) turn into classifying spaces of de Rham cohomology, K-theory and (conjecturally) topological modular forms. This describes joint work with Stolz and partially Hohnhold, Kreck and others. |
| Speaker: Ben Webster Title: Categorification, Lie algebras and topology (Slides) It's a long established principle that an interesting way to think about numbers as the sizes of sets or dimensions of vector spaces, or better yet, the Euler characteristic of complexes. You can't have a map between numbers, but you can have one between sets or vector spaces. For example, Euler characteristic of topological spaces is not functorial, but homology is. One can try to extend this idea to a bigger stage, by, say, taking a vector space, and trying to make a category by defining morphisms between its vectors. This approach (interpreted suitably) has been a remarkable success with the representation theory of semi-simple Lie algebras (and their associated quantum groups). I'll give an introduction to this area, with a view toward applications in topology; in particular to replacing polynomial invariants of knots that come from representation theory with vector space valued invariants that reduce to knot polynomials under Euler characteristic. |
| Speaker: Katrin
Wehrheim (Slides) Title: 3-dimensional manifolds and symplectic categories A Lagrangian correspondence is a Lagrangian submanifold in the product of two symplectic manifolds. This generalizes the notion of a symplectomorphism and was introduced by Weinstein in an attempt to build a symplectic category. In joint work with Chris Woodward we define such a category in which all Lagrangian correspondences are composable morphisms. We extend it to a 2-category by extending Floer homology to cyclic sequences of Lagrangian correspondences. This is based on counts of 'holomorphic quilts' - a collection of holomorphic curves in different manifolds with 'seam values' in the Lagrangian correspondences. A fundamental isomorphism of Floer homologies ensures that our constructions are compatible with the geometric composition of Lagrangian correspondences. This provides a general prescription for constructing topological invariants by decomposition into simple pieces and a partial functor into the symplectic category (which need only be defined on simple pieces; with moves corresponding to geometric composition). |
| Speaker: Edward
Witten Title: Gauge Theory And Khovanov Homology (Slides, Lecture Notes) I will describe how the Jones polynomial and Khovanov homology can be computed by counting the solutions of certain elliptic differential equations on a four- or five-dimensional manifold with boundary. |
Any Questions? Comments? Contact: ianagol@math.berkeley.edu