The main application of interface methods to fluid mechanics is to track an evolving interface. This is done by viewing the boundary as an interface, and then using level set methods to keep track of the boundary. The advantage of this approach is three-fold.

• First, it is easy to evaluate quantities such as the local curvature which determine the surface tension of the interface separating different fluids.
• Second, because of the ability of these techniques to allow topological changes in the evolving front, differing regions can merge and split apart.
• Third, the approach is unchanged in three dimensions and higher.

Once the position and geometry of the interface is determined, one has to solve the Navier-Stokes equations for fluid flow. This may be done through a variety of techniques, most typically using Chorin's projection method.

The final, and most delicate issue is the coupling of the interface to these flow solvers. This is best done through the notion of extension velocities which allow a seamless and accurate technique for coupling the dynamics of the interface to the solutions of the relevant Navier-Stokes equations on either side of the interface. The central idea is to view the interface as altering the right-hand-side of the equations of motion, and solving for the fluid velocity everywhere, and then using the extension velocity ideas to advance the interface. Done in this manner, the method conserves mass, and avoids the ad-hoc and artificial technique of constant re-initialization of the

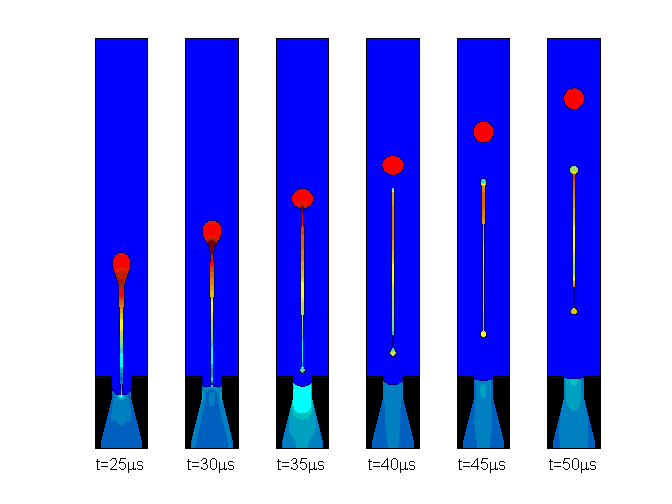
InkJet Simulations

Some of the most recent and exciting work has to do with simulation of inkjet plotters, both for Newtonian flow and Non-Newtonian viscoelastic flow The goal of this work is to develop a numerical simulation tool for fluid flow phenomena associated with ink jet printers. The physical goal is to analyze the motion of the boundary, pinch off of droplets, formation of satellites, and the effect of nozzle geometry on ink ejection size and motion. These extra satellites break off because of the role of surface tension along the air/ink boundary: the ejected bubble elongates and then pinches off.

In order to accurately simulate this process, the underlying algorithms should be able to faithfully discretize non-rectangular geometries, accurately capture two-phase flows through an axisymmetric nozzle, handle complicated topological change of ink droplets, conserve mass to a good approximation, and couple to external models which simulate the ink cartridge, supply channel, pressure chamber, and piezoelectric actuator.

Annotated References:

• Reference 1 is an early attempt to couple level set methods to the problem of fluids with compressible fluid flows.
• Reference 2 is couples projection methods for fluid flows to level set methods; this is done in the context of a combustion problem in which the motion of a flame in a swirling, vorticity-driven flow is studied. The flame is cold, in that there is no feedback from the flame dynamics to the fluid solver.
• Reference 3 is Chorin's seminal paper on projection methods for computing viscous flow.
• Reference 4 is a second order version of the projection scheme which is the current state-of-the-art.
• References 5,6 and 7 couple level set methods to projection methods for solving two-phase flow problems. The central idea here is the feedback mechanism between the level set view and the fluid solver.
• Reference 8 provides a general, all-purpose approach for connecting most physics problems involving interfaces to level set methods.
• Reference 9 is a review article from the Annual Review of Fluid Mechanics.
• References 10, 11 and 12 discuss the application of these techniques to modeling ink jet plotters and viscoelastic flow.

Examples:

Movie of Rising Thermal	Ink Jet Plotter

A special page on fluid mechanics

A special page on inkjet plotters

A special page on ViscoElastic Flow

References:

1. Computing Interface Motion in Compressible Gas Dynamics : Mulder, W., Osher, S.J., Sethian, J.A., Jour. Comp. Phys., 100, pp. 209--228, 1992.

   Abstract

   need abstract

   Download publications

   
   
2. Projection Methods Coupled to Level Set Interface Techniques : Zhu, J. and Sethian, J.A., J. Comp. Phys., 102, pp. 128--138, 1992.

   Abstract

   In this paper, we merge modern techniques for computing the solution to the viscous Navier-Stokes equations with modern techniques for computing the motion of interfaces propagating with curvature-dependent speeds. The resulting algorithm tracks the motion of an evolving interface in a complex flow field, and easily handles complex changes in the front, including the development of spikes and cusps, topological changes and breaking/merging. As examples, we apply the resulting algorithm to interface boundaries in a driven cavity and in a shear layer, and cold flame propagation in a hydrodynamic field.

   Download publications

   
   

3. Numerical Solution of the Navier-Stokes Equations : Chorin, A.J., Math. Comp., 22, pp. 745, 1968.

   Download publications

   
   

4. A Second-Order Projection Method for the Incompressible Navier-Stokes Equations : Bell, J.B., Colella, P., and Glaz, H.M., J. Comp. Phys., 85, pp. 257--283, 1989.

   Download publications

   
   

5. A Level Set Formulation of Eulerian Interface Capturing Methods for Incompressible Fluid Flows : Chang, Y.C., Hou, T.Y., Merriman, B., and Osher, S.J., Jour. Comp. Phys., 124, pp. 449-464, 1996.

   Download publications

   
   

6. A Level Set Method for Computing Solutions to Incompressible Two-Phase Flow : Sussman, M., Smereka, P. and Osher, S.J., J. Comp. Phys. 114, pp. 146--159, 1994.

   Download publications

   
   

7. Tracking Two-Phase Flow Problems in Two and Three Dimensions : Zhu, J. and Sethian, J.A., in progress.

   Download publications

   
   

8. The Fast Construction of Extension Velocities in Level Set Methods : Adalsteinsson, D., and Sethian, J.A., J. Comp. Phys., 148, 1999, pp. 2-22.

   Abstract

   Level set techniques are numerical techniques for tracking the evolution of interfaces. They rely on two central embeddings; first the embedding of the interface as the zero level set of a higher dimensional function, and second, the embedding (or extension) of the interface's velocity to this higher dimensional level set function. This paper applies Sethian's Fast Marching Method, which is a very fast technique for solving the Eikonal and related equations, to the problem of building fast and appropriate extension velocities for the neighboring level sets. Our choice and construction of extension velocities serves several purposes. First, it provides a way of building velocities for neighboring level sets in the cases where the velocity is defined only on the front itself. Second, it provides a sub-grid resolution in some cases not present in the standard level set approach. Third, it provides a way to update an interface according to a given velocity field prescribed on the front in such a way that the signed distance function is maintained, and the front is never re-initialized; this is valuable in many complex simulations. In this paper, we describe the details of such implementations, together with speed and convergence tests, and applications to problems in visibility relevant to semi--conductor manufacturing and thin film physics.

   Download publications

   
   

   
   
9. Level Set Methods for Fluid Interfaces : Sethian, J.A., and Smereka, P., Annual Review of Fluid Mechanics, 35, pp.341-372, 2003.

   Abstract

   A large collection of fluid problems involve moving interfaces. Applications include air-water dynamics, breaking surface waves, solidification melt dynamics, and combustion and reacting flows. In many such applications, the interplay between the interface dynamics and the surrounding fluid motion is subtle, with factors such as density ratios and temperature jumps across the interface, surface tension effects, topological connectivity and boundary conditions playing significant roles in the dynamics.
   
   Over the past fifteen years, a class of numerical techniques known as level set methods have been built to tackle some of the most complex problems in fluid interface motion. Level set methods, introduced by Osher and Sethian, are computational techniques for tracking moving interfaces; they rely on an implicit representation of the interface whose equation of motion is numerically approximated using schemes built from those for hyperbolic conservation laws. The resulting techniques are able to handle problems in which the speed of the evolving interface may sensitively depend on local properties such as curvature and normal direction, as well as complex physics off the front and internal jump and boundary conditions determined by the interface location. Level set methods are particularly designed for problems in multiple space dimensions in which the topology of the evolving interface changes during the course of events, and problems in which sharp corners and cusps are present.
   
   In this review, we discuss the numerical development of these techniques and their application to a collection of problems in fluid mechanics, including incompressible and compressible flow, and applications to bubble dynamics, ship hydrodynamics, and inkjet printhead design. We note that there already exists a collection of review articles and books on these techniques, and refer the interested reader to works by Osher and Fedkiw (2001) and Sethian (1996b 1996c, 1999a, 1999b, 2001).

   Download publications

   
   
10. A Coupled Level Set Projection Method Applied to Ink Jet Simulation : Yu, J-D., Sakai, S., and Sethian, J.A., Interfaces and Free Boundaries, 193, No. 1, pp 275-305, 2003,

    Abstract

    A finite difference level set-projection method on rectangular grid is developed for piezoelectric ink jet simulation. The model is based on the Navier-Stokes equations for incompressible two-phase flows in the presence of surface tension and density jump across the interface separating ink and air, coupled to an electric circuit model which describes the driving mechanism behind the process, and a macroscopic contact model which describes the air-ink-wall dynamics. We simulate the axisymmetric flow using a combination of second order projection methods to solve the fluid equations and level set methods to track the air/ink interface. The numerical method can be used to analyze the motion of the interface, breakoff and formation of satellites, and effect of nozzle geometry on droplet size and motion. We focus on close comparison of our numerical ink jet simulation with experimental data.

    Download publications

    
    
11. A Coupled Quadrilateral Grid Level Set Projection Method Applied to Ink Jet Simulation : Yu, J.D., Sakai, S., and Sethian, J.A., J. Computational Physics, 206, 1, pp. 227-251, 2005

    Abstract

    A coupled level set-projection method on quadrilateral grids is developed for piezoelectric ink jet simulations. The model is based on the Navier-Stokes equations for incompressible two-phase flows in the presence of surface tension and density jump across the interface separating ink and air, coupled to an electric circuit model which describes the driving mechanism behind the process, and a macroscopic contact model which describes the air-ink-wall dynamics. We simulate the axisymmetric flow on quadrilateral grids using a combination of second-order finite difference projection methods to solve the fluid equations and level set methods to track the air/ink interface. To improve the mass conservation performance of the coupled level set method, a bicubic interpolation is combined with the fast marching method for level set re-initialization on quadrilateral grids. The numerical method is used to analyze the motion of the interface, droplet pinch off, formation of satellites, effect of nozzle geometry on droplet size and motion, and the dynamics for droplet landing. The simulations are faithful to the dimensions and physics of a particular class of inkjet devices.

    Download publications

    
    
12. Two-Phase Viscoelastic Jetting : Yu, J.D., Sakai, S., and Sethian, J.A., to appear, J. Computational Physics, 2006

    Abstract

    A coupled finite difference algorithm on rectangular grids is developed for viscoelastic ink ejection simulations. The ink is modeled by the Oldroyd-B viscoelastic fluid model. The coupled algorithm seamlessly incorporates several things: (1) a coupled level set-projection method for incompressible immiscible two-phase fluid flows; (2) a higher-order Godunov type algorithm for the convection terms in the momentum and level set equations; (3) a simple first-order upwind algorithm for the convection term in the viscoelastic stress equations; (4) central difference approximations for viscosity, surface tension, and upper-convected derivative terms; and (5) an equivalent circuit model to calculate the inflow pressure (or flow rate) from dynamic voltage.

    Download publications