OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
Coupling Level Set Methods to Physical Problems
You are currently in the
topic outlined in red.
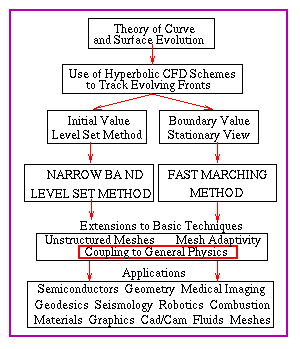
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
Coupling to General Physics
In order to couple level set methods to most physical applications,
one must link the position and motion of the interface to physical
effects on one or both sides of the interface. This linking often
requires solving relevant partial differential equations on either side
of the front, and employs jump boundary conditions at the interface
itself. Thus, the position of the front influences the physics, and the
physics then prescribes the motion of the interface.
In order to develop a general level set implementation of such problems,
we need to make an important observation.
The
Narrow Band level set methods
contains two embeddings. First, the propagating interface is
embedded as the zero level set of the higher dimensional level set
function. This allows one to track topological changes in the interface,
and calculate geometric quantities from the smooth level set function.
Equally important, the speed F of the interface in its normal direction
is embedded in this higher dimensional view; an extension speed function
F_ext
must be defined must be defined in a neighborhood of the zero level set.
In other words, we must extend the speed F off of the interface to
the neighboring level sets.
The choice of which extension to use is crucial. While tempting to
use those given by the underlying physics (such as, for example,
the fluid velocity away from the front), this leads to poor results,
including the loss of mass and inaccuracy. Remedies to repair these
errors through so-called "re-initialization techniques" (that is,
stopping the calculation every time step and building a wholly new level set
function) are fraught with their own problems; they can change
the position of the interface.
Adding Material Transport
Narrow Band level set methods
track the trace of the propagating front: all information about
the original parameterization is lost. This is the reason it handles
topological changes so effortlessly. However, sometimes additional quantities
are carried by transport along the front, and these are required in order
to correctly solve the associated physics.
To handle this problem, a new technique is used to carry an additional
embedded function, defined in all of space. The time-evolution
partial differential equation for this function is solved as part of the
simultaneous update along with the level set advancement.
Annotated References:
In Ref. 1 below, a general technique was presented to build extension
velocities, based only on the value of the speed function F on the front.
This choice of extension velocity
F_ext
moves the interface under the correct speed, and can be shown to keep
the smoothness of the interface as it evolves. The equation that gives
this extension velocity may be quickly solved using the
Fast Marching Method
.
This provides a general way to couple level set methods to physical problems.
In Ref. 2 below, the idea of adding an additional embedded function to
carry material transport is discussed.
New Book and Resource on Level Set and Fast Marching Methods
References:
-
The Fast Construction of Extension Velocities in
Level Set Methods
: Adalsteinsson, D., and Sethian, J.A.,
148, pp. 2-22, 1999.
Abstract
Level set techniques are numerical techniques for tracking the
evolution of interfaces. They rely on two central embeddings;
first the embedding of the interface as the zero level set of a
higher dimensional function, and second, the embedding (or
extension) of the interface's velocity to this
higher dimensional level set function.
This paper applies Sethian's Fast Marching Method, which is a very fast
technique for solving the Eikonal and related equations, to the
problem of building fast and appropriate extension velocities
for the neighboring level sets.
Our choice and construction of extension velocities serves several
purposes. First, it provides a way of building velocities for
neighboring level sets in the cases where the velocity is defined
only on the front itself.
Second, it provides a sub-grid resolution in some cases not present in the
standard level set approach.
Third, it provides a way to update an interface
according to a given velocity
field prescribed on the front in such a way that the signed distance
function is maintained, and the front is never re-initialized; this
is valuable in many complex simulations.
In this paper, we describe the details of such implementations,
together with speed and convergence tests, and applications
to problems in visibility relevant to semi--conductor manufacturing and
thin film physics.
Download publications
To handle this problem, a new technique is used to carry an additional embedded function, defined in all of space. The time-evolution partial differential equation for this function is solved as part of the simultaneous update along with the level set advancement.
Annotated References:
In Ref. 1 below, a general technique was presented to build extension
velocities, based only on the value of the speed function F on the front.
This choice of extension velocity
F_ext
moves the interface under the correct speed, and can be shown to keep
the smoothness of the interface as it evolves. The equation that gives
this extension velocity may be quickly solved using the
Fast Marching Method
.
This provides a general way to couple level set methods to physical problems.
In Ref. 2 below, the idea of adding an additional embedded function to
carry material transport is discussed.
New Book and Resource on Level Set and Fast Marching Methods
References:
-
The Fast Construction of Extension Velocities in
Level Set Methods
: Adalsteinsson, D., and Sethian, J.A.,
148, pp. 2-22, 1999.
Abstract
Level set techniques are numerical techniques for tracking the
evolution of interfaces. They rely on two central embeddings;
first the embedding of the interface as the zero level set of a
higher dimensional function, and second, the embedding (or
extension) of the interface's velocity to this
higher dimensional level set function.
This paper applies Sethian's Fast Marching Method, which is a very fast
technique for solving the Eikonal and related equations, to the
problem of building fast and appropriate extension velocities
for the neighboring level sets.
Our choice and construction of extension velocities serves several
purposes. First, it provides a way of building velocities for
neighboring level sets in the cases where the velocity is defined
only on the front itself.
Second, it provides a sub-grid resolution in some cases not present in the
standard level set approach.
Third, it provides a way to update an interface
according to a given velocity
field prescribed on the front in such a way that the signed distance
function is maintained, and the front is never re-initialized; this
is valuable in many complex simulations.
In this paper, we describe the details of such implementations,
together with speed and convergence tests, and applications
to problems in visibility relevant to semi--conductor manufacturing and
thin film physics.
Download publications
New Book and Resource on Level Set and Fast Marching Methods
Abstract
Level set techniques are numerical techniques for tracking the
evolution of interfaces. They rely on two central embeddings;
first the embedding of the interface as the zero level set of a
higher dimensional function, and second, the embedding (or
extension) of the interface's velocity to this
higher dimensional level set function.
This paper applies Sethian's Fast Marching Method, which is a very fast
technique for solving the Eikonal and related equations, to the
problem of building fast and appropriate extension velocities
for the neighboring level sets.
Our choice and construction of extension velocities serves several
purposes. First, it provides a way of building velocities for
neighboring level sets in the cases where the velocity is defined
only on the front itself.
Second, it provides a sub-grid resolution in some cases not present in the
standard level set approach.
Third, it provides a way to update an interface
according to a given velocity
field prescribed on the front in such a way that the signed distance
function is maintained, and the front is never re-initialized; this
is valuable in many complex simulations.
In this paper, we describe the details of such implementations,
together with speed and convergence tests, and applications
to problems in visibility relevant to semi--conductor manufacturing and
thin film physics.
Download publications
Level set techniques are numerical techniques for tracking the evolution of interfaces. They rely on two central embeddings; first the embedding of the interface as the zero level set of a higher dimensional function, and second, the embedding (or extension) of the interface's velocity to this higher dimensional level set function. This paper applies Sethian's Fast Marching Method, which is a very fast technique for solving the Eikonal and related equations, to the problem of building fast and appropriate extension velocities for the neighboring level sets. Our choice and construction of extension velocities serves several purposes. First, it provides a way of building velocities for neighboring level sets in the cases where the velocity is defined only on the front itself. Second, it provides a sub-grid resolution in some cases not present in the standard level set approach. Third, it provides a way to update an interface according to a given velocity field prescribed on the front in such a way that the signed distance function is maintained, and the front is never re-initialized; this is valuable in many complex simulations. In this paper, we describe the details of such implementations, together with speed and convergence tests, and applications to problems in visibility relevant to semi--conductor manufacturing and thin film physics.
Adalsteinsson, D., and Sethian, J.A., J. Comp. Phys, 185, 1, pp. 271-288, 2002
Abstract
We develop theory and numerical algorithms to apply level set methods
to problems involving the transport and diffusion of material quantities
in a level set framework. Level set methods are computational
techniques for tracking moving interfaces; they work by embedding the
propagating interface as the zero level set of a higher dimensional
function, and then approximate the solution of the resulting initial
value partial differential equation using upwind finite difference
schemes. The traditional level set method works in the trace space of the
evolving interface, and hence disregards any parameterization
in the interface description. Consequently, material quantities on
the interface which themselves are transported under the interface motion
are not easily handled in this framework.
We develop model equations and algorithmic techniques to extend the
level set method to include these problems. We demonstrate the accuracy of
our approach through a series of test examples and convergence studies.
Download publications
We develop theory and numerical algorithms to apply level set methods to problems involving the transport and diffusion of material quantities in a level set framework. Level set methods are computational techniques for tracking moving interfaces; they work by embedding the propagating interface as the zero level set of a higher dimensional function, and then approximate the solution of the resulting initial value partial differential equation using upwind finite difference schemes. The traditional level set method works in the trace space of the evolving interface, and hence disregards any parameterization in the interface description. Consequently, material quantities on the interface which themselves are transported under the interface motion are not easily handled in this framework. We develop model equations and algorithmic techniques to extend the level set method to include these problems. We demonstrate the accuracy of our approach through a series of test examples and convergence studies.