OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
Fast Marching Methods and Ordered Upwind Methods
You are currently in the
topic outlined in red.
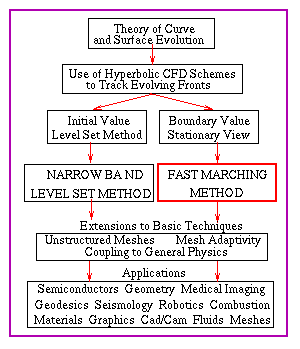
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
Fast Marching Methods
Fast Marching Methods are the optimal way to solve the Eikonal equationwhich arise in a variety of applications, including front propagation problems in which a front propagates normal to itself with a speed F which depends only on position and is always positive. This includes applications in optics, seismology, path planning and robotic navigation, photolitography and electromagnetics. Introduced in Ref. 1 below, they produce the first arrival viscosity solution of the stationary Hamilton-Jacobi equation.
The techniques rely on upwind schemes, the theory of viscosity solutions, causality, and sort algorithms borrowed from computer science. They compute the solution to the Eikonal equation in O(N log N) steps, where N is the total number of points in the computational domain. As well as providing optimal techniques for solving a collection of physical problems, they also provide ways of building and computing extension velocities which are required to couple level set methods to complex physics.
Ordered Upwind Methods
Fast Marching Methods are designed to track a propagating interface, and find the first arrival of the interface as it passes a point. They also are designed for problems in which the speed of propagation is isotropic: this means that standing at any point, you get to move in any direction with the same speed. That speed can change from point to point, but once you dropped in the domain, there's no preferred direction. This was the setting for the problem of robotic navigation, in which we found the optimal path through and around a set of obstacles.In optimal control , how much it costs to move depends on both where you are standing and also on the direction in which you chose to move. A good example is sailing: the direction of the wind gives a preferred direction, and your speed depends on which direction you choose. There are many physical examples of this, including preferred directions in the etching of microchips and anisotropic propagation of waves in rock.
Unfortunately, the Fast Marching Method won't work in this setting. The answer why has to do with how the method really works. In the Fast Marching Method, just like Dijkstra's method, one systematically updates the solution starting from known values, and works from known territory to unknown spots. At each step, one exploits the fact that the perpendicular (or gradient) back to the front is the direction from which information must come. Mathematically, this means that the characteristics are the same as the gradient. The way out of this, that is, the way to keep the idea of Dijkstra's method and a one-pass algorithm is to keep track of the ratio between the fastest and slowest speed at each point. This anisotropy ratio reveals something important: although the information may not come along a trajectory perpendicular to the front, it can't come from very far away. In the figure below, the only trajectories on the front that can send information to the green spot are those that start no further than the anisotropy ratio times the distance to the closest point.
This means that one can keep the entire Dijkstra-like one-pass metholodogy, only now it can be extended to anisotropic speeds. These methods are called Ordered Upwind Methods, because they maintain an ordering of the points and systematically compute the solution by relying on known, previously computed information which lies upstream. This means that one can keep the entire Dijkstra-like one-pass metholodogy, only now it can be extended to anisotropic speeds. These methods are called Ordered Upwind Methods, because they maintain an ordering of the points and systematically compute the solution by relying on known, previously computed information which lies upstream.
(
A general introduction, images, and movies about Fast Marching Methods
)
Connections to other works:
The Fast Marching Method evolved in part from examining the limit
of the narrow band method as the band was reduced to one grid cell.
Fast Marching Methods, by taking the perspective of the large body of work on
higher order upwind, finite difference approximants from
hyperbolic conservation laws, allow for higher order versions
on both structured and unstructured meshes.
At their core, Fast Marching Methods are most closely related to
Dijkstra's method (Ref. 4), which is a classic algorithm for computing the
shortest path on a network of links. It too relies on a heap to find
the smallest element of the expanding front, and can be thought of
as a Huyghen's principle algorithm where the expanding wave is
confined to the network paths. It can also be thought of as an upwind
finite difference scheme, however the equation it is solving is not
the same as the Eikonal equation, and hence the paths it produces are
non-unique, unlike the Fast Marching Method.
The Fast Marching Method is an upwind finite difference scheme
which produces the correct viscosity solution to the Eikonal
equation through a causality
relationship based on the order of the upwinding.
Tsitsikilis was the first to develop a Dijkstra-like method for
solving the Eikonal equation: his was a control theory approach (as opposed
to the Fast Marching upwind finite difference perspective) to solving the
Eikonal equation: it is also a viscosity solution with the same operation
count.
This leads to a causality relationship based on the optimality criterion rather
than on the upwind finite difference operators employed in Fast
Marching Methods.
In the particular special case of a first order upwind finite difference
for the Fast Marching Method on a square mesh, the resulting update equation
at each grid point can be seen to be the same quadratic equation obtained
through Tsitsikilis's control theoretic approach.
There are similarities and differences between this method and the Fast
Marching Method: for a detailed examination, see Ref #6 below.
Annotated References:
-
Ref #1 below introduces Fast Marching Methods, discusses the causality
relationship and heap structure which gives the method its underlying
speed, and applies it to problems in photolithography development.
-
Ref. #2 further discusses the technique, and applies it to a host
of applications.
-
Ref. #3 shows how to build higher order Fast Marching Methods,
using switch functions and higher order stencils; it tests the accuracy
of these algorithms on several examples.
-
Ref. #4 introduces Ordered Upwind Methods, which are one-pass Dijkstra-like
methods for computing the solution to static convex first-order
Hamilton-Jacobi equations. It extends Fast Marching Methods to include
anisotropic problems in which the speed depends not only on position but
also on direction.
-
Ref. #5 develops Ordered Upwind Methods for general hybrid continuous-discrete
control.
-
Ref. #6 presents the theory and numerics behind Ordered Upwind Methods in
depth. It presents both semi-Langrangian and fully Eulerian techniques, and
discusses in detail the similarities and differences between Tsitsiklis'
Method and the Fast Marching Method, and provides a wide collection of
applications of Ordered Upwind Methods to problems in optimal control.
New Book and Resource on Level Set and Fast Marching Methods
References:
-
A Fast Marching Level Set Method for Monotonically
Advancing Fronts
: Sethian, J.A.,
Proc. Nat. Acad. Sci., 93, 4, pp.1591-1595, 1996.
Abstract
We present a fast marching level set method for monotonically advancing
fronts, which leads to an extremely fast scheme for solving the Eikonal
equation.
Level set methods are numerical techniques for computing the
position of propagating fronts.
They rely on an initial value partial differential equation for
a propagating level set function, and use techniques borrowed from
hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
In this paper, we describe a particular case of such methods for
interfaces whose speed depends only on local position.
The technique works by coupling work on entropy conditions for
interface motion, the theory of viscosity solutions for Hamilton-Jacobi
equations and fast adaptive narrow band level set methods.
The technique is applicable to a variety of problems, including
shape-from-shading problems, lithographic development calculations
in microchip manufacturing, and arrival time problems in control theory.
Download publications
-
Theory, Algorithms, and Applications of Level Set Methods for Propagating
Interfaces,
: Sethian, J.A.,
Acta Numerica, Cambridge University
Press, 1996.
Abstract
We review recent work on level set methods for following the
evolution of complex interfaces. These techniques are based on solving an
initial value partial differential equations for a level set functions,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
The methodology results in robust, accurate, and efficient numerical
algorithms for propagating interfaces in highly complex settings.
We review the basic theory and approximations, describe a hierarchy of
fast methods, including an extremely fast marching level set scheme for
monotonically advancing fronts, based on a stationary formulation of
the problem, and discuss extensions to multiple
interfaces and triple points. Finally, we demonstrate the
technique applied to a series of examples from geometry, material science and
computer vision, including mean curvature flow, minimal surfaces,
grid generation, fluid mechanics, and combustion.
Download publications
-
Fast Marching Methods
: Sethian, J.A.,
SIAM Review, 41, July, 1999
Abstract
Fast Marching Methods are numerical schemes for computing
the solution of the non-linear Eikonal equation and
related static Hamilton-Jacobi equations.
They provide consistent, accurate, and highly efficient
techniques, and are based on entropy-satisfying upwind schemes and
fast sorting techniques.
The computational complexity of the algorithms is $O(N \log N)$,
where $N$ is the total number of points in the domain.
These schemes are of use in a variety of applications,
including problems in shape offsetting,
computing distances from complex curves and surfaces,
shape-from-shading, photolithography development,
computing first arrivals in seismic travel times, construction
of shortest geodesics on surfaces, optimal path planning around
obstacles, and visibility and reflection calculations.
In this paper, we review the development of these
techniques, including the theoretical and numerical underpinnings,
provide details of the computational schemes, and demonstrate
the techniques in a collection of different areas.
Download publications
-
Ordered Upwind Methods for Static Hamilton-Jacobi Equations
:
Sethian, J.A., and Vladimirsky, A.,
Proceedings of the National Academy of Sciences,
98, 11069-11074, 2001.
Abstract
We introduce a family of fast Ordered Upwind Methods (OUMs)
for approximating
solutions to a wide class of static Hamilton-Jacobi equations with
Dirichlet boundary conditions.
Standard techniques often rely on iteration to converge to the
solution of a discretized version of the partial differential equation.
Our new fast methods avoid iteration through a careful use of
the information about the characteristic directions of the underlying PDE.
These techniques are of complexity O( M log M), where M is the
total number of points in the domain.
We consider anisotropic test problems in optimal control, seismology,
and paths on surfaces.
Download publications
-
Ordered Upwinds Methods for Hybrid Control
:
Sethian, J.A., and Vladimirsky, A.,
Proceedings Fifth International Conference on Hybrid Systems and Control,
Ed. C. Tomlin and M.R. Greenstreet, LCNS 2289, Springer, pp. 393, 2002
Abstract
We introduce a family of highly efficient (non-iterative) numerical
methods for a wide class of hybrid control systems.
The application of Dijkstra's classical method to a discrete optimal
trajectory
problem on a network obtains the solution in $O( M \log M)$ operations.
The key idea behind the method is a careful use of the direction
of information propagation, stemming from the optimality principle.
In a series of recent papers, we have introduced a number of
Ordered Upwind Methods (OUMs) to efficiently solve the fully anisotropic
continuous optimal control problems.
These techniques rely on using a partial information on the characteristic
directions of the Hamilton--Jacobi--Bellman PDE,
stemming from the continuous variant of the optimality principle.
The resulting non-iterative algorithms have the computational
complexity of $O( M \log M)$, where $M$ is the total number of grid points
where the solution is computed, regardless of the dimension of
the control/state variables.
In this paper, we show how Ordered Upwind Methods may be extended
to efficiently solve the hybrid (discrete/continuous) control problems.
We illustrate our methods by solving a series of hybrid
optimal trajectory problems with and without time-dependence
of the speed function.
Download publications
-
Ordered Upwind Methods for Static Hamilton-Jacobi Equations: Theory
and Algorithms
:
Sethian, J.A., and Vladimirsky, A.,
SIAM J. Numer. Anal., 41, 1, pp. 325-363, 2003
Abstract
We develop a family of fast methods to approximate the solutions
to a wide class of static Hamilton-Jacobi partial differential
equations. Numerical solutions to these problems are typically obtained
by solving a large system of coupled non-linear
discretized equations.
Our techniques, which we refer to as
``Ordered Upwind Methods'' (OUM), use partial information
about the characteristic directions to de-couple these non-linear systems,
greatly reducing the computational labor.
Our techniques are considered in the context of control-theoretic and
front-propagation problems.
We begin by discussing existing ordered upwind methods, focussing on
two designed for
isotropic problems.
We then introduce a new class of
ordered upwind methods which decouple systems for general
(anisotropic) problems. We prove
convergence of one such scheme to the viscosity solution of the corresponding
Hamilton-Jacobi partial differential equation.
Next, we introduce a set of hybrid methods based on an analysis of
the role played by anisotropy in the context of
front propagation and optimal trajectory problems.
The performance of the methods is analyzed and compared to that of
several other numerical approaches to these problems.
Finally, computational experiments are performed using
test problems from control theory, computational geometry and
seismology.
Download publications
-
A Note on Two Problems in Connection with Graphs,
:
Dijkstra, E.W.,
Numerische Mathematic, 1:269--271, 1959.
-
Efficient Algorithms for Globally Optimal Trajectories
:
Tsitsiklis, J.N.,
IEEE Transactions on Automatic Control, Volume 40, pp. 1528-1538, 1995.
The Fast Marching Method evolved in part from examining the limit of the narrow band method as the band was reduced to one grid cell. Fast Marching Methods, by taking the perspective of the large body of work on higher order upwind, finite difference approximants from hyperbolic conservation laws, allow for higher order versions on both structured and unstructured meshes. At their core, Fast Marching Methods are most closely related to Dijkstra's method (Ref. 4), which is a classic algorithm for computing the shortest path on a network of links. It too relies on a heap to find the smallest element of the expanding front, and can be thought of as a Huyghen's principle algorithm where the expanding wave is confined to the network paths. It can also be thought of as an upwind finite difference scheme, however the equation it is solving is not the same as the Eikonal equation, and hence the paths it produces are non-unique, unlike the Fast Marching Method. The Fast Marching Method is an upwind finite difference scheme which produces the correct viscosity solution to the Eikonal equation through a causality relationship based on the order of the upwinding.
Tsitsikilis was the first to develop a Dijkstra-like method for solving the Eikonal equation: his was a control theory approach (as opposed to the Fast Marching upwind finite difference perspective) to solving the Eikonal equation: it is also a viscosity solution with the same operation count. This leads to a causality relationship based on the optimality criterion rather than on the upwind finite difference operators employed in Fast Marching Methods. In the particular special case of a first order upwind finite difference for the Fast Marching Method on a square mesh, the resulting update equation at each grid point can be seen to be the same quadratic equation obtained through Tsitsikilis's control theoretic approach. There are similarities and differences between this method and the Fast Marching Method: for a detailed examination, see Ref #6 below.
Annotated References:
-
Ref #1 below introduces Fast Marching Methods, discusses the causality
relationship and heap structure which gives the method its underlying
speed, and applies it to problems in photolithography development.
-
Ref. #2 further discusses the technique, and applies it to a host
of applications.
-
Ref. #3 shows how to build higher order Fast Marching Methods,
using switch functions and higher order stencils; it tests the accuracy
of these algorithms on several examples.
-
Ref. #4 introduces Ordered Upwind Methods, which are one-pass Dijkstra-like
methods for computing the solution to static convex first-order
Hamilton-Jacobi equations. It extends Fast Marching Methods to include
anisotropic problems in which the speed depends not only on position but
also on direction.
-
Ref. #5 develops Ordered Upwind Methods for general hybrid continuous-discrete
control.
-
Ref. #6 presents the theory and numerics behind Ordered Upwind Methods in
depth. It presents both semi-Langrangian and fully Eulerian techniques, and
discusses in detail the similarities and differences between Tsitsiklis'
Method and the Fast Marching Method, and provides a wide collection of
applications of Ordered Upwind Methods to problems in optimal control.
New Book and Resource on Level Set and Fast Marching Methods
References:
-
A Fast Marching Level Set Method for Monotonically
Advancing Fronts
: Sethian, J.A.,
Proc. Nat. Acad. Sci., 93, 4, pp.1591-1595, 1996.
Abstract
We present a fast marching level set method for monotonically advancing
fronts, which leads to an extremely fast scheme for solving the Eikonal
equation.
Level set methods are numerical techniques for computing the
position of propagating fronts.
They rely on an initial value partial differential equation for
a propagating level set function, and use techniques borrowed from
hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
In this paper, we describe a particular case of such methods for
interfaces whose speed depends only on local position.
The technique works by coupling work on entropy conditions for
interface motion, the theory of viscosity solutions for Hamilton-Jacobi
equations and fast adaptive narrow band level set methods.
The technique is applicable to a variety of problems, including
shape-from-shading problems, lithographic development calculations
in microchip manufacturing, and arrival time problems in control theory.
Download publications
-
Theory, Algorithms, and Applications of Level Set Methods for Propagating
Interfaces,
: Sethian, J.A.,
Acta Numerica, Cambridge University
Press, 1996.
Abstract
We review recent work on level set methods for following the
evolution of complex interfaces. These techniques are based on solving an
initial value partial differential equations for a level set functions,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
The methodology results in robust, accurate, and efficient numerical
algorithms for propagating interfaces in highly complex settings.
We review the basic theory and approximations, describe a hierarchy of
fast methods, including an extremely fast marching level set scheme for
monotonically advancing fronts, based on a stationary formulation of
the problem, and discuss extensions to multiple
interfaces and triple points. Finally, we demonstrate the
technique applied to a series of examples from geometry, material science and
computer vision, including mean curvature flow, minimal surfaces,
grid generation, fluid mechanics, and combustion.
Download publications
-
Fast Marching Methods
: Sethian, J.A.,
SIAM Review, 41, July, 1999
Abstract
Fast Marching Methods are numerical schemes for computing
the solution of the non-linear Eikonal equation and
related static Hamilton-Jacobi equations.
They provide consistent, accurate, and highly efficient
techniques, and are based on entropy-satisfying upwind schemes and
fast sorting techniques.
The computational complexity of the algorithms is $O(N \log N)$,
where $N$ is the total number of points in the domain.
These schemes are of use in a variety of applications,
including problems in shape offsetting,
computing distances from complex curves and surfaces,
shape-from-shading, photolithography development,
computing first arrivals in seismic travel times, construction
of shortest geodesics on surfaces, optimal path planning around
obstacles, and visibility and reflection calculations.
In this paper, we review the development of these
techniques, including the theoretical and numerical underpinnings,
provide details of the computational schemes, and demonstrate
the techniques in a collection of different areas.
Download publications
-
Ordered Upwind Methods for Static Hamilton-Jacobi Equations
:
Sethian, J.A., and Vladimirsky, A.,
Proceedings of the National Academy of Sciences,
98, 11069-11074, 2001.
Abstract
We introduce a family of fast Ordered Upwind Methods (OUMs)
for approximating
solutions to a wide class of static Hamilton-Jacobi equations with
Dirichlet boundary conditions.
Standard techniques often rely on iteration to converge to the
solution of a discretized version of the partial differential equation.
Our new fast methods avoid iteration through a careful use of
the information about the characteristic directions of the underlying PDE.
These techniques are of complexity O( M log M), where M is the
total number of points in the domain.
We consider anisotropic test problems in optimal control, seismology,
and paths on surfaces.
Download publications
-
Ordered Upwinds Methods for Hybrid Control
:
Sethian, J.A., and Vladimirsky, A.,
Proceedings Fifth International Conference on Hybrid Systems and Control,
Ed. C. Tomlin and M.R. Greenstreet, LCNS 2289, Springer, pp. 393, 2002
Abstract
We introduce a family of highly efficient (non-iterative) numerical
methods for a wide class of hybrid control systems.
The application of Dijkstra's classical method to a discrete optimal
trajectory
problem on a network obtains the solution in $O( M \log M)$ operations.
The key idea behind the method is a careful use of the direction
of information propagation, stemming from the optimality principle.
In a series of recent papers, we have introduced a number of
Ordered Upwind Methods (OUMs) to efficiently solve the fully anisotropic
continuous optimal control problems.
These techniques rely on using a partial information on the characteristic
directions of the Hamilton--Jacobi--Bellman PDE,
stemming from the continuous variant of the optimality principle.
The resulting non-iterative algorithms have the computational
complexity of $O( M \log M)$, where $M$ is the total number of grid points
where the solution is computed, regardless of the dimension of
the control/state variables.
In this paper, we show how Ordered Upwind Methods may be extended
to efficiently solve the hybrid (discrete/continuous) control problems.
We illustrate our methods by solving a series of hybrid
optimal trajectory problems with and without time-dependence
of the speed function.
Download publications
-
Ordered Upwind Methods for Static Hamilton-Jacobi Equations: Theory
and Algorithms
:
Sethian, J.A., and Vladimirsky, A.,
SIAM J. Numer. Anal., 41, 1, pp. 325-363, 2003
Abstract
We develop a family of fast methods to approximate the solutions
to a wide class of static Hamilton-Jacobi partial differential
equations. Numerical solutions to these problems are typically obtained
by solving a large system of coupled non-linear
discretized equations.
Our techniques, which we refer to as
``Ordered Upwind Methods'' (OUM), use partial information
about the characteristic directions to de-couple these non-linear systems,
greatly reducing the computational labor.
Our techniques are considered in the context of control-theoretic and
front-propagation problems.
We begin by discussing existing ordered upwind methods, focussing on
two designed for
isotropic problems.
We then introduce a new class of
ordered upwind methods which decouple systems for general
(anisotropic) problems. We prove
convergence of one such scheme to the viscosity solution of the corresponding
Hamilton-Jacobi partial differential equation.
Next, we introduce a set of hybrid methods based on an analysis of
the role played by anisotropy in the context of
front propagation and optimal trajectory problems.
The performance of the methods is analyzed and compared to that of
several other numerical approaches to these problems.
Finally, computational experiments are performed using
test problems from control theory, computational geometry and
seismology.
Download publications
-
A Note on Two Problems in Connection with Graphs,
:
Dijkstra, E.W.,
Numerische Mathematic, 1:269--271, 1959.
-
Efficient Algorithms for Globally Optimal Trajectories
:
Tsitsiklis, J.N.,
IEEE Transactions on Automatic Control, Volume 40, pp. 1528-1538, 1995.
New Book and Resource on Level Set and Fast Marching Methods
Abstract
We present a fast marching level set method for monotonically advancing
fronts, which leads to an extremely fast scheme for solving the Eikonal
equation.
Level set methods are numerical techniques for computing the
position of propagating fronts.
They rely on an initial value partial differential equation for
a propagating level set function, and use techniques borrowed from
hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
In this paper, we describe a particular case of such methods for
interfaces whose speed depends only on local position.
The technique works by coupling work on entropy conditions for
interface motion, the theory of viscosity solutions for Hamilton-Jacobi
equations and fast adaptive narrow band level set methods.
The technique is applicable to a variety of problems, including
shape-from-shading problems, lithographic development calculations
in microchip manufacturing, and arrival time problems in control theory.
Download publications
We present a fast marching level set method for monotonically advancing fronts, which leads to an extremely fast scheme for solving the Eikonal equation. Level set methods are numerical techniques for computing the position of propagating fronts. They rely on an initial value partial differential equation for a propagating level set function, and use techniques borrowed from hyperbolic conservation laws. Topological changes, corner and cusp development, and accurate determination of geometric properties such as curvature and normal direction are naturally obtained in this setting. In this paper, we describe a particular case of such methods for interfaces whose speed depends only on local position. The technique works by coupling work on entropy conditions for interface motion, the theory of viscosity solutions for Hamilton-Jacobi equations and fast adaptive narrow band level set methods. The technique is applicable to a variety of problems, including shape-from-shading problems, lithographic development calculations in microchip manufacturing, and arrival time problems in control theory.
Abstract
We review recent work on level set methods for following the
evolution of complex interfaces. These techniques are based on solving an
initial value partial differential equations for a level set functions,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
The methodology results in robust, accurate, and efficient numerical
algorithms for propagating interfaces in highly complex settings.
We review the basic theory and approximations, describe a hierarchy of
fast methods, including an extremely fast marching level set scheme for
monotonically advancing fronts, based on a stationary formulation of
the problem, and discuss extensions to multiple
interfaces and triple points. Finally, we demonstrate the
technique applied to a series of examples from geometry, material science and
computer vision, including mean curvature flow, minimal surfaces,
grid generation, fluid mechanics, and combustion.
Download publications
We review recent work on level set methods for following the evolution of complex interfaces. These techniques are based on solving an initial value partial differential equations for a level set functions, using techniques borrowed from hyperbolic conservation laws. Topological changes, corner and cusp development, and accurate determination of geometric properties such as curvature and normal direction are naturally obtained in this setting. The methodology results in robust, accurate, and efficient numerical algorithms for propagating interfaces in highly complex settings. We review the basic theory and approximations, describe a hierarchy of fast methods, including an extremely fast marching level set scheme for monotonically advancing fronts, based on a stationary formulation of the problem, and discuss extensions to multiple interfaces and triple points. Finally, we demonstrate the technique applied to a series of examples from geometry, material science and computer vision, including mean curvature flow, minimal surfaces, grid generation, fluid mechanics, and combustion.
Abstract
Fast Marching Methods are numerical schemes for computing
the solution of the non-linear Eikonal equation and
related static Hamilton-Jacobi equations.
They provide consistent, accurate, and highly efficient
techniques, and are based on entropy-satisfying upwind schemes and
fast sorting techniques.
The computational complexity of the algorithms is $O(N \log N)$,
where $N$ is the total number of points in the domain.
These schemes are of use in a variety of applications,
including problems in shape offsetting,
computing distances from complex curves and surfaces,
shape-from-shading, photolithography development,
computing first arrivals in seismic travel times, construction
of shortest geodesics on surfaces, optimal path planning around
obstacles, and visibility and reflection calculations.
In this paper, we review the development of these
techniques, including the theoretical and numerical underpinnings,
provide details of the computational schemes, and demonstrate
the techniques in a collection of different areas.
Download publications
Fast Marching Methods are numerical schemes for computing the solution of the non-linear Eikonal equation and related static Hamilton-Jacobi equations. They provide consistent, accurate, and highly efficient techniques, and are based on entropy-satisfying upwind schemes and fast sorting techniques. The computational complexity of the algorithms is $O(N \log N)$, where $N$ is the total number of points in the domain. These schemes are of use in a variety of applications, including problems in shape offsetting, computing distances from complex curves and surfaces, shape-from-shading, photolithography development, computing first arrivals in seismic travel times, construction of shortest geodesics on surfaces, optimal path planning around obstacles, and visibility and reflection calculations. In this paper, we review the development of these techniques, including the theoretical and numerical underpinnings, provide details of the computational schemes, and demonstrate the techniques in a collection of different areas.
Abstract
We introduce a family of fast Ordered Upwind Methods (OUMs)
for approximating
solutions to a wide class of static Hamilton-Jacobi equations with
Dirichlet boundary conditions.
Standard techniques often rely on iteration to converge to the
solution of a discretized version of the partial differential equation.
Our new fast methods avoid iteration through a careful use of
the information about the characteristic directions of the underlying PDE.
These techniques are of complexity O( M log M), where M is the
total number of points in the domain.
We consider anisotropic test problems in optimal control, seismology,
and paths on surfaces.
Download publications
We introduce a family of fast Ordered Upwind Methods (OUMs) for approximating solutions to a wide class of static Hamilton-Jacobi equations with Dirichlet boundary conditions. Standard techniques often rely on iteration to converge to the solution of a discretized version of the partial differential equation. Our new fast methods avoid iteration through a careful use of the information about the characteristic directions of the underlying PDE. These techniques are of complexity O( M log M), where M is the total number of points in the domain. We consider anisotropic test problems in optimal control, seismology, and paths on surfaces.
Abstract
We introduce a family of highly efficient (non-iterative) numerical
methods for a wide class of hybrid control systems.
The application of Dijkstra's classical method to a discrete optimal
trajectory
problem on a network obtains the solution in $O( M \log M)$ operations.
The key idea behind the method is a careful use of the direction
of information propagation, stemming from the optimality principle.
In a series of recent papers, we have introduced a number of
Ordered Upwind Methods (OUMs) to efficiently solve the fully anisotropic
continuous optimal control problems.
These techniques rely on using a partial information on the characteristic
directions of the Hamilton--Jacobi--Bellman PDE,
stemming from the continuous variant of the optimality principle.
The resulting non-iterative algorithms have the computational
complexity of $O( M \log M)$, where $M$ is the total number of grid points
where the solution is computed, regardless of the dimension of
the control/state variables.
In this paper, we show how Ordered Upwind Methods may be extended
to efficiently solve the hybrid (discrete/continuous) control problems.
We illustrate our methods by solving a series of hybrid
optimal trajectory problems with and without time-dependence
of the speed function.
Download publications
We introduce a family of highly efficient (non-iterative) numerical
methods for a wide class of hybrid control systems.
The application of Dijkstra's classical method to a discrete optimal
trajectory
problem on a network obtains the solution in $O( M \log M)$ operations.
The key idea behind the method is a careful use of the direction
of information propagation, stemming from the optimality principle.
In a series of recent papers, we have introduced a number of
Ordered Upwind Methods (OUMs) to efficiently solve the fully anisotropic
continuous optimal control problems.
These techniques rely on using a partial information on the characteristic
directions of the Hamilton--Jacobi--Bellman PDE,
stemming from the continuous variant of the optimality principle.
The resulting non-iterative algorithms have the computational
complexity of $O( M \log M)$, where $M$ is the total number of grid points
where the solution is computed, regardless of the dimension of
the control/state variables.
In this paper, we show how Ordered Upwind Methods may be extended
to efficiently solve the hybrid (discrete/continuous) control problems.
We illustrate our methods by solving a series of hybrid
optimal trajectory problems with and without time-dependence
of the speed function.
Abstract
We develop a family of fast methods to approximate the solutions
to a wide class of static Hamilton-Jacobi partial differential
equations. Numerical solutions to these problems are typically obtained
by solving a large system of coupled non-linear
discretized equations.
Our techniques, which we refer to as
``Ordered Upwind Methods'' (OUM), use partial information
about the characteristic directions to de-couple these non-linear systems,
greatly reducing the computational labor.
Our techniques are considered in the context of control-theoretic and
front-propagation problems.
We begin by discussing existing ordered upwind methods, focussing on
two designed for
isotropic problems.
We then introduce a new class of
ordered upwind methods which decouple systems for general
(anisotropic) problems. We prove
convergence of one such scheme to the viscosity solution of the corresponding
Hamilton-Jacobi partial differential equation.
Next, we introduce a set of hybrid methods based on an analysis of
the role played by anisotropy in the context of
front propagation and optimal trajectory problems.
The performance of the methods is analyzed and compared to that of
several other numerical approaches to these problems.
Finally, computational experiments are performed using
test problems from control theory, computational geometry and
seismology.
Download publications
We develop a family of fast methods to approximate the solutions
to a wide class of static Hamilton-Jacobi partial differential
equations. Numerical solutions to these problems are typically obtained
by solving a large system of coupled non-linear
discretized equations.
Our techniques, which we refer to as
``Ordered Upwind Methods'' (OUM), use partial information
about the characteristic directions to de-couple these non-linear systems,
greatly reducing the computational labor.
Our techniques are considered in the context of control-theoretic and
front-propagation problems.
We begin by discussing existing ordered upwind methods, focussing on
two designed for
isotropic problems.
We then introduce a new class of
ordered upwind methods which decouple systems for general
(anisotropic) problems. We prove
convergence of one such scheme to the viscosity solution of the corresponding
Hamilton-Jacobi partial differential equation.
Next, we introduce a set of hybrid methods based on an analysis of
the role played by anisotropy in the context of
front propagation and optimal trajectory problems.
The performance of the methods is analyzed and compared to that of
several other numerical approaches to these problems.
Finally, computational experiments are performed using
test problems from control theory, computational geometry and
seismology.