The above work on Narrow Band level set methods and Fast Marching Methods relies on rectangular Cartesian meshes. In fact, the entire methodology can be moved to unstructured meshes, employing the work on upwind methods on unstructured simplices developed over the past decade.


Annotated References:

• Ref #1 develops the entire level set methodology for unstructured meshes. It shows how to build a variety of schemes, analyzes their accuracy, discusses extensions to include curvature, and applies the resulting algorithms to problems in etching and deposition in microchip manufacturing. The methods are discussed for general Hamilton-Jacobi equations.
  
  
• Ref. #2 uses these upwind operators and theory to develop a first order Fast Marching Methods in two dimensions on unstructured meshes, and uses this technique to compute shortest path geodesics on manifolds.
  
  
• Ref. #3 shows how to build second order unstructured Fast Marching Methods, and extends the technique to three space dimensions.
  
  
• Ref. #4 reviews some of this work.

New Book and Resource on Level Set and Fast Marching Methods



References:

1. Numerical Schemes for the Hamilton-Jacobi and Level Set Equations on Triangulated Domains : Barth, T.J., and Sethian, J.A., Journal of Computational Phys., 145, 1, pp. 1-40, 1998.

   Abstract

   Borrowing from techniques developed for conservation law equations, numerical schemes which discretize the Hamilton-Jacobi (H-J), level set, and Eikonal equations on triangulated domains are presented. The first scheme is a provably monotone discretization for the H-J equations. Unfortunately, the basic scheme lacks proper Lipschitz continuity of the numerical Hamiltonian. By employing a ``virtual'' edge flipping technique, Lipschitz continuity of the numerical flux is restored on acute triangulations. Next, schemes are introduced and developed based on the weaker concept of positive coefficient approximations for homogeneous Hamiltonians. These schemes possess a discrete maximum principle on arbitrary triangulations and naturally exhibit Lipschitz continuity of the numerical Hamiltonian under mild assumptions on the data and Hamiltonian. Finally, a class of Petrov-Galerkin approximations are considered. These schemes are stabilized via a least-squares bilinear form. The Petrov-Galerkin schemes do not possess a discrete maximum principle but generalize to high order accuracy. Discretization of the level set equation also requires the numerical approximation of a mean curvature term. A simple mass-lumped Galerkin approximation is presented and analyzed using maximum principle analysis. The use of unstructured meshes permits several forms of mesh adaptation which have been incorporated into numerical examples. These numerical examples include discretizations of convex and nonconvex forms of the H-J equation, the Eikonal equation, and the level set equation.

   Download publications

   
   
2. Fast Marching Methods on Triangulated Domains : Kimmel, R., and Sethian, J.A., Proc. Nat. Acad. Sci., 95, pp. 8341-8435, 1998.

   Abstract

   The Fast Marching Method is a numerical algorithm for solving the Eikonal equation on a rectangular orthogonal mesh in $O(M \log M)$ steps, where $M$ is the total number of grid points. In this paper we extend the Fast Marching Method to triangulated domains with the same computational complexity. As an application, we provide an optimal time algorithm for computing the geodesic distances and thereby extracting shortest paths on triangulated manifolds.

   Download publications

   
   
3. Fast Methods for the Eikonal and Related Hamilton-Jacobi Equations on Unstructured Meshes : Sethian, J.A. and Vladimirsky, A., Proceedings of the National Academy of Sciences, 97, pp. 5699-5703, 2000.

   Abstract

   The Fast Marching Method is a numerical algorithm for solving the Eikonal equation on a rectangular orthogonal mesh in O(M log M) steps, where M is the total number of grid points. The scheme relies on an upwind finite difference approximations to the gradient and a resulting causality relationship which lends itself to a Dijkstra-like programming approach. In this paper we discuss several extensions to this technique, including higher order versions on unstructured meshes in R^n and on manifolds, connections to more general static Hamilton-Jacobi equations, and links to more general problems in optimal control.

   Download publications

   
   
4. Implementation of Hamilton-Jacobi and Level Set Equations on Triangulated Domains : Barth, T.J., and Sethian, J.A. von Karman Institute Lecture Series, Computational Fluid Mechanics, 1998.

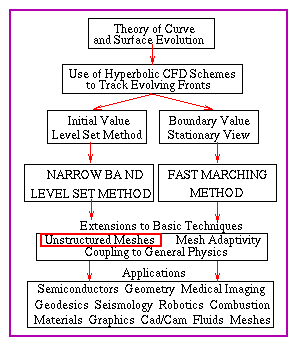
   Abstract

   In the previous article, we discussed level set and Fast Marching Methods on Cartesian meshes. In this paper, we review the extension of much of the methodology to triangulated domains; in particular, we discuss a collection of schemes for solving general Hamilton-Jacobi and level set equations in a triangulated and finite element framework. The first scheme is a provably monotone discretization for certain forms of the H-J equations. While this basic scheme lacks proper Lipschitz continuity of the numerical Hamiltonian, it can be restored on acute triangulations through a ``virtual'' edge flipping technique. Next, schemes are presented based on the weaker concept of positive coefficient approximations for homogeneous Hamiltonians. These schemes possess a discrete maximum principle on arbitrary triangulations and naturally exhibit proper Lipschitz continuity of the numerical Hamiltonian. These schemes are followed by a Petrov-Galerkin scheme from a traditional finite element setting. We also discuss the addition and numerical approximation of a mean curvature term. Finally, we review several forms of mesh adaptation, and present some numerical examples. Complete details about triangulated Hamilton-Jacobi solvers may be found in the article by Barth and Sethian.

   In this paper, we discuss extensions to the basic method. We present higher order versions of these techniques for both Cartesian and unstructured meshes in both two and three space dimensions. We cast the method in a general framework, and provide accuracy tests and new applications of the underlying techniques.

   Download publications