OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
Applications to Robotics and Path Navigation
You are currently in the
topic outlined in red.
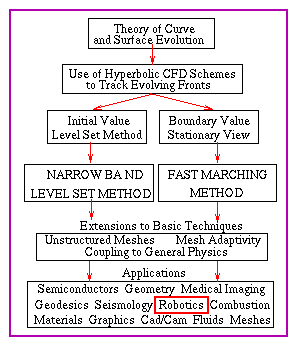
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
where T is the arrival time and F(x,y,theta) is the speed at a point (x,y,theta) taken as zero if the object cannot enter that point. This is similar to the application of computing shortest geodesic paths on manifold in that one uses the Fast Marching Method to find the arrival time solution and then traces backwards along the gradient to produce the shortest path. The resulting algorithm is O(N log N), where N is the number of points in the computational domain, making it a highly efficient technique.
Reference 1 below shows how these techniques may be applied to problems in path planning. The interested reader is referred to
Example:

|

|
| (51K) | (71K) |
(see Reference 1 below)
Design your own obstacle course and robot
New Book and Resource on Level Set and Fast Marching Methods
References:
-
Application of Fast Marching Methods to Path
Planning
: Kimmel, R., and Sethian, J.A.,
Center for Pure and Applied Mathematics Report,
Univ. of California, Berkeley, May 1996.
Abstract
We present a consistent, accurate, and efficient numerical scheme for solving problems in path planning. Our approach is based on Sethian's Fast Marching Method, which is a fast algorithm for solving static Hamilton-Jacobi equations, and is based on entropy-satisfying upwind schemes and fast sorting techniques. The computational complexity of this algorithm is $O(N \log N)$, where $N$ is the total number of points in configuration space. The Fast Marching Method is comparable to graph-search algorithms in complexity, however, because the scheme is stable and consistent. That is, the scheme is guaranteed to converge to the optimal path as the grid is refined. Once the Eikonal equation is solved, the optimal path is extracted using back propagation through the associated field of arrival times. We demonstrate the algorithm by accurately computing optimal paths for problems with 2 and 3 degrees of freedom. The scheme is applicable to path planning problems with a relatively small number of space dimension; in problems with a large number of degrees of freedom, memory limitations are substantial.
Download publications