OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
Applications to Materials Sciences
You are currently in the
topic outlined in red.
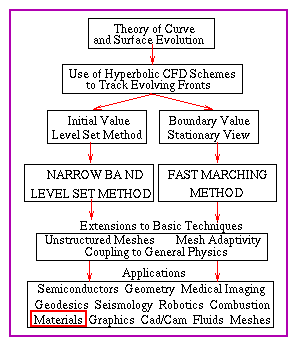
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
The application of
level set methods
and
Fast Marching Methods
to materials sciences problems is a natural fit. As before, the
central idea is to use view material boundaries as zero level sets
of higher dimensional functions, and to track the evolving interfaces.
Typical examples include solid-liquid boundaries, boundaries in metal
layers in etching and deposition, photolithography development
simulations, and solid-gas boundaries.
-
Refs. 1,2 and 3 are the examples of applying
level set methods
to crystal growth. They study interface stability in
crystal growth and dendritic solidification, and includes the
effects of heat release, Gibbs-Thomson boundary conditions,
curvature-depedent heat terms, and anisotropic effects.
Ref. 1 transforms the problem to a boundary integral formulation,
and then extends an appropriate velocity field off of the interface
to allow the update of neighboring level sets.
The results show a wide variety of physical effects, including
tip-splitting, side-branching, unstable growth and effects of
container boundary conditions.
Ref. 3 takes a different approach; rather than use a boundary
integral formulation, it works directly with the diffusion
equation in both regimes.
-
Refs. 4,5,6,7 and 8 discuss the application of interface
techniques to problems in
etching and deposition in semiconductor manufacturing
.
These are some of the most involved applications of
level set
and
Fast Marching Methods
to date. They study the effects of material-dependent etch rates,
non-linear flux laws, visibility calculations, surface diffusion,
and re-deposition/re-emission on the evolving surface profiles.
- Ref. 9 studies the application of level set methods to optimal
structural design, showing how to build schemes which construct efficient
design of weight-bearing structures.
- Refs. 10, 11 and 12 study the metallization failure, electromigration, and the
growth of voids due to vacancy fluxes and transport. Previous work
using this approach includes the work of Zhao. et. al. and the work of
Averbuch, Israeli and Ravve. These techniques combines immersed
interface methods for solving the irregular Poisson problems around
the voids,
level set methods to track the interface,
Fast Marching Methods to extend the velocity and update the
neighboring level sets. The results show the growth of voids, merger,
and the effects of the various terms.
New Book and Resource on Level Set and Fast Marching Methods
References:
-
Crystal Growth and Dendritic Solidification
:
Sethian, J.A., and Strain, J.D.,
Journal of Computational Physics, 98, pp. 231-253, 1992.
Abstract
We present a numerical method
which computes the motion of
complex solid/liquid boundaries
in crystal growth.
The model we solve includes physical effects such as
crystalline anisotropy, surface tension,
molecular kinetics and undercooling.
The method is based on two ideas.
First, the equations of motion are recast
as a single history-dependent
boundary integral equation on the solid/liquid boundary.
A fast algorithm is used to solve
the integral equation efficiently.
Second, the boundary is moved by solving
a "Hamilton-Jacobi"-type equation (on a
fixed domain)
formulated by Osher and Sethian for a function in which the boundary
is a particular level set.
This equation is solved by finite difference schemes
borrowed from the technology
of hyperbolic conservation laws.
The two ideas are combined by constructing a
smooth extension of the normal velocity
off the moving boundary,
in a way suggested by the physics of the problem.
Our numerical experiments
show the evolution of complex crystalline shapes,
development of large spikes and corners,
dendrite formation and side-branching,
and pieces of solid merging and breaking off freely.
-
Algorithms for Computing Crystal Growth and
Dendritic Solidification
: Sethian, J.A. and Strain, J.D.,
Institute of Mathematics and its Applications, University of Minnesota,
pp. 107-126 (1992).
Abstract
We report on a numerical method for computing
the motion of complex solid/liquid boundaries
in crystal growth.
The model we solve includes physical effects such as
crystalline anisotropy, surface tension,
molecular kinetics and undercooling.
The method is based on a single single history-dependent boundary integral
equation on the solid/liquid boundary, which is solved by means
f a fast algorithm coupled to
a level set approach for tracking the evolving boundary.
Numerical experiments show the evolution of complex crystalline shapes,
development of large spikes and corners,
dendrite formation and side-branching,
and pieces of solid merging and breaking off freely.
Download publications
-
A Simple Level Set Method for Solving Stefan Problem
:
Chen, S., Merriman, B., Osher, S., and Smereka, P.,
Journal of Computational Physics, 138, pp. 8-29, 1997.
-
A Level Set Approach to a Unified Model for
Etching, Deposition, and Lithography I: Algorithms and Two-Dimensional
Simulations
: Adalsteinsson, D,. and Sethian, J.A.,
Journal of Computational Physics, 120, 1, pp. 128--144, 1995.
Abstract
We apply a level set formulation to the problem of surface advancement
in a two-dimensional topography simulation of deposition, etching,
and lithography processes in integrated circuit fabrication.
The level set formulation is based on solving
a Hamilton-Jacobi type equation for a propagating level set function,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting. The equations of motion of a unified
model, including the effects of isotropic and unidirectional deposition
and etching, visibility, surface diffusion, reflection, and material
dependent etch/deposition rates are presented and adapted to a level set
formulation. The development of this model and algorithm naturally extends
to three dimensions in a straightforward manner, and is
described in Part II of this paper.
Download publications
-
A Level Set Approach to a Unified Model for Etching, Deposition,
and Lithography II: Three-Dimensional Simulations
: Adalsteinsson, D., and Sethian, J.A.,
Journal of Computational Physics,
122, 2, pp. 348--366, 1995.
Abstract
We apply a level set formulation to the problem of surface advancement
in three-dimensional topography simulation of deposition, etching,
and lithography processes in integrated circuit fabrication.
The level set formulation is based on solving
a Hamilton-Jacobi type equation for a propagating level set function,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting. The equations of motion of a unified
model, including the effects of isotropic and unidirectional deposition
and etching, visibility, surface diffusion, reflection, and material
dependent etch/deposition rates are presented and adapted to a level set
formulation. In Part I of this paper, the basic equations and algorithms
for two dimensional simulations were developed. In this paper, the
extension to three dimensions is presented. We show a large collection
of simulations, including three-dimensional etching and deposition into
cavities under the effects of visibility, directional and source flux
functions, evolution of lithographic profiles, discontinuous etch rates
In Part III of this paper, effects of reflection, re-emission,
surface diffusion, and multiple materials will be presented.
Download publications
-
A Level Set Approach to a Unified Model for Etching,
Deposition,
and Lithography III:
Re-Deposition, Re-Emission, Surface Diffusion, and Complex
Simulations
:
Adalsteinsson, D., and Sethian, J.A.,
Journal of Computational Physics, 138, 1, pp. 193-223, 1997.
Abstract
Previously, Adalsteinsson and Sethian have applied the level set formulation
to the problem of
surface advancement in two and three-dimensional topography simulation of
deposition, etching, and lithography processes in integrated circuit
fabrication. The level set formulation is based on solving
a Hamilton-Jacobi type equation for a propagating level set function,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
Part I presented the basic equations and algorithms
for two dimensional simulations, including the effects of
isotropic and uni-directional deposition
and etching, visibility, reflection, and material
dependent etch/deposition rates.
Part II focused on the
extension to three dimensions.
This paper completes the series, and add the effects of
re-deposition, re-emission, and surface diffusion.
This requires the solution of the
transport equations for arbitrary geometries, and leads to simulations that
contain multiple simultaneous competing effects of
visibility, directional and source flux
coefficients for the re-emission and re-deposition
functions, multi-layered fronts and thin film layers.
Download publications
-
Fast Marching Level Set Methods for
Three Dimensional Photolithography
: Sethian, J.A.,
Proceedings, SPIE 1996 International Symposium on Microlithography, Santa
Clara, California, March, 1996.
Abstract
We present detailed timings of a
fast marching level set method
introduced by Sethian for surface
advancement in photoresist development. The method merges
fast narrow band
level set methods
entropy-satisfying schemes for the
Eikonal equation, and fast heap sort algorithms.
The resulting method can perform the development stage of the
three-dimensional photoresist process in 80 seconds on a
Sparc10 for a 200x200x200 grid.
Download publications
-
An Overview of Level Set Methods for Etching,
Deposition, and Lithography
: Sethian, J.A., and Adalsteinsson, D.,
IEEE Transactions on Semiconductor Devices, 1996.
10, 1, pp.167-184, 1997.
Abstract
The range of surface evolution problems in etching, deposition, and
lithography development offers significant challenge for numerical
methods in front tracking. Level set methods for evolving interfaces
are specifically designed for profiles which can develop sharp corners,
change topology, and undergo orders of magnitude changes in speed.
They are based on solving a Hamilton-Jacobi type equation for a level set
function, using techniques borrowed from hyperbolic conservation laws.
Over the past few years, a body of level set methods have been
developed with application to microfabrication problems.
In this paper, we give an overview of
these techniques, describe the implementation in etching, deposition, and
lithography simulations, and present a collection of fast level set methods,
each aimed at a particular application. In the case of photoresist development
and isotropic etching/deposition,
the fast marching level set method}}, introduced
by Sethian,
can track the three-dimensional photoresist process through a
$200 \times 200 \times 200$ rate function grid in under 55 seconds on a
Sparc10.
In the case of more complex etching and deposition,
the Narrow Band level set method, introduced in by Adalsteinsson and
Sethian, can be used to handle problems in which the speed of the interface
delicately depends on the orientation of the interface vs. an incoming
beam, the effects of visibility, surface tension, reflection and
re-emission, and complex three-dimensional effects.
Our applications include photoresist development, etching/deposition
problems under the effects of masking, visibility, complex flux integrations
over sources, non-convex sputter deposition problems, and simultaneous
deposition and etch phenomena.
Download publications
-
Structural Boundary Design via Level Set and Immersed Interfaces Methods
:
Sethian, J.A., and Wiegmann, A.,
J. Comp. Phys., 163, 2, Sep 2000, pp. 489-528
Abstract
Download publications
-
A numerical model of stress driven grain boundary diffusion
:
Wilkening, J., and Sethian, J.A.,
J. Comp. Phys.,
193, 1, pp. 275-305, 2003
Download publications
-
Analysis of Stress Driven Grain Boundary Diffusion, Part I
:
Wilkening, J., Borucki, L., and Sethian, J.A.,
SIAM J. Appl. Math., 64, 6, 1839-1863, 2004.
Download publications
-
Analysis of Stress Driven Grain Boundary Diffusion, Part II
:
Wilkening, J., Borucki, L., and Sethian, J.A.,
SIAM J. Appl. Math., 64, 6, 1864-1886, 2004.
Download publications
Additional References:
-
A Simple Level Set Method for Solving Stefan Problem
:
Chen, S., Merriman, B., Osher, S., and Smereka, P.,
Journal of Computational Physics, 138, pp. 8-29, 1997.
New Book and Resource on Level Set and Fast Marching Methods
Abstract
We present a numerical method
which computes the motion of
complex solid/liquid boundaries
in crystal growth.
The model we solve includes physical effects such as
crystalline anisotropy, surface tension,
molecular kinetics and undercooling.
The method is based on two ideas.
First, the equations of motion are recast
as a single history-dependent
boundary integral equation on the solid/liquid boundary.
A fast algorithm is used to solve
the integral equation efficiently.
Second, the boundary is moved by solving
a "Hamilton-Jacobi"-type equation (on a
fixed domain)
formulated by Osher and Sethian for a function in which the boundary
is a particular level set.
This equation is solved by finite difference schemes
borrowed from the technology
of hyperbolic conservation laws.
The two ideas are combined by constructing a
smooth extension of the normal velocity
off the moving boundary,
in a way suggested by the physics of the problem.
Our numerical experiments
show the evolution of complex crystalline shapes,
development of large spikes and corners,
dendrite formation and side-branching,
and pieces of solid merging and breaking off freely.
We present a numerical method which computes the motion of complex solid/liquid boundaries in crystal growth. The model we solve includes physical effects such as crystalline anisotropy, surface tension, molecular kinetics and undercooling. The method is based on two ideas. First, the equations of motion are recast as a single history-dependent boundary integral equation on the solid/liquid boundary. A fast algorithm is used to solve the integral equation efficiently. Second, the boundary is moved by solving a "Hamilton-Jacobi"-type equation (on a fixed domain) formulated by Osher and Sethian for a function in which the boundary is a particular level set. This equation is solved by finite difference schemes borrowed from the technology of hyperbolic conservation laws. The two ideas are combined by constructing a smooth extension of the normal velocity off the moving boundary, in a way suggested by the physics of the problem. Our numerical experiments show the evolution of complex crystalline shapes, development of large spikes and corners, dendrite formation and side-branching, and pieces of solid merging and breaking off freely.
Abstract
We report on a numerical method for computing
the motion of complex solid/liquid boundaries
in crystal growth.
The model we solve includes physical effects such as
crystalline anisotropy, surface tension,
molecular kinetics and undercooling.
The method is based on a single single history-dependent boundary integral
equation on the solid/liquid boundary, which is solved by means
f a fast algorithm coupled to
a level set approach for tracking the evolving boundary.
Numerical experiments show the evolution of complex crystalline shapes,
development of large spikes and corners,
dendrite formation and side-branching,
and pieces of solid merging and breaking off freely.
Download publications
We report on a numerical method for computing the motion of complex solid/liquid boundaries in crystal growth. The model we solve includes physical effects such as crystalline anisotropy, surface tension, molecular kinetics and undercooling. The method is based on a single single history-dependent boundary integral equation on the solid/liquid boundary, which is solved by means f a fast algorithm coupled to a level set approach for tracking the evolving boundary. Numerical experiments show the evolution of complex crystalline shapes, development of large spikes and corners, dendrite formation and side-branching, and pieces of solid merging and breaking off freely.
Abstract
We apply a level set formulation to the problem of surface advancement
in a two-dimensional topography simulation of deposition, etching,
and lithography processes in integrated circuit fabrication.
The level set formulation is based on solving
a Hamilton-Jacobi type equation for a propagating level set function,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting. The equations of motion of a unified
model, including the effects of isotropic and unidirectional deposition
and etching, visibility, surface diffusion, reflection, and material
dependent etch/deposition rates are presented and adapted to a level set
formulation. The development of this model and algorithm naturally extends
to three dimensions in a straightforward manner, and is
described in Part II of this paper.
Download publications
We apply a level set formulation to the problem of surface advancement in a two-dimensional topography simulation of deposition, etching, and lithography processes in integrated circuit fabrication. The level set formulation is based on solving a Hamilton-Jacobi type equation for a propagating level set function, using techniques borrowed from hyperbolic conservation laws. Topological changes, corner and cusp development, and accurate determination of geometric properties such as curvature and normal direction are naturally obtained in this setting. The equations of motion of a unified model, including the effects of isotropic and unidirectional deposition and etching, visibility, surface diffusion, reflection, and material dependent etch/deposition rates are presented and adapted to a level set formulation. The development of this model and algorithm naturally extends to three dimensions in a straightforward manner, and is described in Part II of this paper.
Abstract
We apply a level set formulation to the problem of surface advancement
in three-dimensional topography simulation of deposition, etching,
and lithography processes in integrated circuit fabrication.
The level set formulation is based on solving
a Hamilton-Jacobi type equation for a propagating level set function,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting. The equations of motion of a unified
model, including the effects of isotropic and unidirectional deposition
and etching, visibility, surface diffusion, reflection, and material
dependent etch/deposition rates are presented and adapted to a level set
formulation. In Part I of this paper, the basic equations and algorithms
for two dimensional simulations were developed. In this paper, the
extension to three dimensions is presented. We show a large collection
of simulations, including three-dimensional etching and deposition into
cavities under the effects of visibility, directional and source flux
functions, evolution of lithographic profiles, discontinuous etch rates
In Part III of this paper, effects of reflection, re-emission,
surface diffusion, and multiple materials will be presented.
Download publications
We apply a level set formulation to the problem of surface advancement in three-dimensional topography simulation of deposition, etching, and lithography processes in integrated circuit fabrication. The level set formulation is based on solving a Hamilton-Jacobi type equation for a propagating level set function, using techniques borrowed from hyperbolic conservation laws. Topological changes, corner and cusp development, and accurate determination of geometric properties such as curvature and normal direction are naturally obtained in this setting. The equations of motion of a unified model, including the effects of isotropic and unidirectional deposition and etching, visibility, surface diffusion, reflection, and material dependent etch/deposition rates are presented and adapted to a level set formulation. In Part I of this paper, the basic equations and algorithms for two dimensional simulations were developed. In this paper, the extension to three dimensions is presented. We show a large collection of simulations, including three-dimensional etching and deposition into cavities under the effects of visibility, directional and source flux functions, evolution of lithographic profiles, discontinuous etch rates In Part III of this paper, effects of reflection, re-emission, surface diffusion, and multiple materials will be presented.
Abstract
Previously, Adalsteinsson and Sethian have applied the level set formulation
to the problem of
surface advancement in two and three-dimensional topography simulation of
deposition, etching, and lithography processes in integrated circuit
fabrication. The level set formulation is based on solving
a Hamilton-Jacobi type equation for a propagating level set function,
using techniques borrowed from hyperbolic conservation laws. Topological
changes, corner and cusp development, and accurate determination of
geometric properties such as curvature and normal direction are
naturally obtained in this setting.
Part I presented the basic equations and algorithms
for two dimensional simulations, including the effects of
isotropic and uni-directional deposition
and etching, visibility, reflection, and material
dependent etch/deposition rates.
Part II focused on the
extension to three dimensions.
This paper completes the series, and add the effects of
re-deposition, re-emission, and surface diffusion.
This requires the solution of the
transport equations for arbitrary geometries, and leads to simulations that
contain multiple simultaneous competing effects of
visibility, directional and source flux
coefficients for the re-emission and re-deposition
functions, multi-layered fronts and thin film layers.
Download publications
Previously, Adalsteinsson and Sethian have applied the level set formulation to the problem of surface advancement in two and three-dimensional topography simulation of deposition, etching, and lithography processes in integrated circuit fabrication. The level set formulation is based on solving a Hamilton-Jacobi type equation for a propagating level set function, using techniques borrowed from hyperbolic conservation laws. Topological changes, corner and cusp development, and accurate determination of geometric properties such as curvature and normal direction are naturally obtained in this setting. Part I presented the basic equations and algorithms for two dimensional simulations, including the effects of isotropic and uni-directional deposition and etching, visibility, reflection, and material dependent etch/deposition rates. Part II focused on the extension to three dimensions. This paper completes the series, and add the effects of re-deposition, re-emission, and surface diffusion. This requires the solution of the transport equations for arbitrary geometries, and leads to simulations that contain multiple simultaneous competing effects of visibility, directional and source flux coefficients for the re-emission and re-deposition functions, multi-layered fronts and thin film layers.
Abstract
We present detailed timings of a
fast marching level set method
introduced by Sethian for surface
advancement in photoresist development. The method merges
fast narrow band
level set methods
entropy-satisfying schemes for the
Eikonal equation, and fast heap sort algorithms.
The resulting method can perform the development stage of the
three-dimensional photoresist process in 80 seconds on a
Sparc10 for a 200x200x200 grid.
Download publications
We present detailed timings of a fast marching level set method introduced by Sethian for surface advancement in photoresist development. The method merges fast narrow band level set methods entropy-satisfying schemes for the Eikonal equation, and fast heap sort algorithms. The resulting method can perform the development stage of the three-dimensional photoresist process in 80 seconds on a Sparc10 for a 200x200x200 grid.
Abstract
The range of surface evolution problems in etching, deposition, and
lithography development offers significant challenge for numerical
methods in front tracking. Level set methods for evolving interfaces
are specifically designed for profiles which can develop sharp corners,
change topology, and undergo orders of magnitude changes in speed.
They are based on solving a Hamilton-Jacobi type equation for a level set
function, using techniques borrowed from hyperbolic conservation laws.
Over the past few years, a body of level set methods have been
developed with application to microfabrication problems.
In this paper, we give an overview of
these techniques, describe the implementation in etching, deposition, and
lithography simulations, and present a collection of fast level set methods,
each aimed at a particular application. In the case of photoresist development
and isotropic etching/deposition,
the fast marching level set method}}, introduced
by Sethian,
can track the three-dimensional photoresist process through a
$200 \times 200 \times 200$ rate function grid in under 55 seconds on a
Sparc10.
In the case of more complex etching and deposition,
the Narrow Band level set method, introduced in by Adalsteinsson and
Sethian, can be used to handle problems in which the speed of the interface
delicately depends on the orientation of the interface vs. an incoming
beam, the effects of visibility, surface tension, reflection and
re-emission, and complex three-dimensional effects.
Our applications include photoresist development, etching/deposition
problems under the effects of masking, visibility, complex flux integrations
over sources, non-convex sputter deposition problems, and simultaneous
deposition and etch phenomena.
Download publications
The range of surface evolution problems in etching, deposition, and
lithography development offers significant challenge for numerical
methods in front tracking. Level set methods for evolving interfaces
are specifically designed for profiles which can develop sharp corners,
change topology, and undergo orders of magnitude changes in speed.
They are based on solving a Hamilton-Jacobi type equation for a level set
function, using techniques borrowed from hyperbolic conservation laws.
Over the past few years, a body of level set methods have been
developed with application to microfabrication problems.
In this paper, we give an overview of
these techniques, describe the implementation in etching, deposition, and
lithography simulations, and present a collection of fast level set methods,
each aimed at a particular application. In the case of photoresist development
and isotropic etching/deposition,
the fast marching level set method}}, introduced
by Sethian,
can track the three-dimensional photoresist process through a
$200 \times 200 \times 200$ rate function grid in under 55 seconds on a
Sparc10.
In the case of more complex etching and deposition,
the Narrow Band level set method, introduced in by Adalsteinsson and
Sethian, can be used to handle problems in which the speed of the interface
delicately depends on the orientation of the interface vs. an incoming
beam, the effects of visibility, surface tension, reflection and
re-emission, and complex three-dimensional effects.
Our applications include photoresist development, etching/deposition
problems under the effects of masking, visibility, complex flux integrations
over sources, non-convex sputter deposition problems, and simultaneous
deposition and etch phenomena.
Abstract
Download publications