OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
Applications to Geometry
You are currently in the
topic outlined in red.
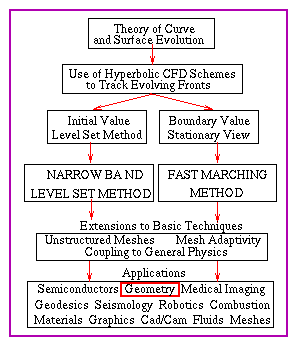
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
A variety of geometry problems have been studied using these techniques, as well as theoretical results about curve and surface evolution. These include minimal surfaces, construction of geodesic shortest paths, flow under the second derivative of curvature and surface diffusion, and the construction of self-similar surfaces.
Annotated References:
-
Ref. 1 studies Grayson's theorem, and is the first study of the
collapse of a dumbell in three dimensions evolving under its mean
curvature. It studies singularity development and blowup.
- Ref. 2 shows how to construct minimal surfaces for arbitrary bounding curves by flowing embedded surfaces under curvature subject to boundary conditions. It is the first use of the narrow band idea.
- Ref. 3 shows how to build a family of self-similar surfaces, whose shape remains unchanged as they move under curvature flow.
- Ref. 4 extends these ideas to multiple singularities, and shows how to construct shortest path geodesics on manifolds.
- Ref. 5 shows how to use a triangulated Fast Marching Method to construct geodesic shortest paths on arbitrary manifolds.
- Ref. 6 studies singularity development in three-dimensional mean curvature flow.
- Ref. 7 gives a computed non-uniqueness result.
- Ref. 8 shows how to combine level set and Fast Marching ideas to build stable algorithms for computing flow under the second derivative of curvature.
-
Refs. 9,10,11, and 12 are theoretical results built using these
level set ideas.
New Book and Resource on Level Set and Fast Marching Methods
Example:
Flow under curvature evolves any simple closed curve to a collapsing circle.
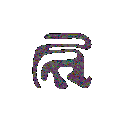
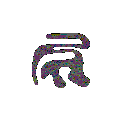
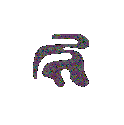
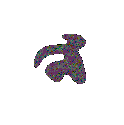
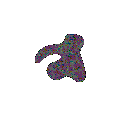
Movie of the above curve collapsing
General explanations, movies, simulations, java applets and details about geometric flow.
General resource on Level Set and Fast Marching Methods
References:
-
Recent Numerical Algorithms for
Hypersurfaces Moving with Curvature-dependent Speed:
Hamilton-Jacobi Equations and Conservation Laws
: Sethian, J.A.,
Journal of Differential Geometry, 31, pp. 131--161, 1990.
Abstract
In many physical problems, interfaces move with a speed that depends on the local curvature. Some common examples are flame propagation, crystal growth, and oil-water boundaries. We idealize the front as a closed, non-intersecting, initial hypersurface flowing along its gradient field with a speed that depends on the curvature. Because explicit solutions seldom exist, numerical approximations are often used. In this paper, we review some recent work on algorithms for attacking these problems. We show that algorithms based on direct parameterizations of the moving front face considerable difficulties. This is because such algorithms adhere to local properties of the solution, rather than the global structure. Conversely, the global properties of the motion can be captured by embedding the surface in a higher-dimensional function. In this setting, the equations of motion can be solved using numerical techniques borrowed from hyperbolic conservation laws. We apply the algorithms to a variety of complicated shapes, showing corner formation and breaking and merging, and conclude with a study of a dumbbell in #R sup 3# moving under its mean curvature. We follow the collapsing dumbbell as the handle pinches off, a singularity develops, and the front breaks into two separate surfaces.
Download publications
-
Computing Minimal Surfaces via Level Set Curvature
Flow
: Chopp, D.L.
Journal of Computational Physics, 106, pp. 77-91, 1993.
Download publications
-
Numerical Computation of Self-Similar Solutions for Mean Curvature
: Chopp, D.L.,
Journal of Experimental Mathemtatics, 3, 1, pp. 1-15, 1994.
Download publications
-
Flow Under Curvature: Singularity Formation,
Minimal Surfaces, and Geodesics
: Chopp, D.L., and Sethian, J.A.,
Jour.
Exper. Math., 2, 4, pp. 235--255, 1993.
Abstract
We study hypersurfaces moving under flow that depends on the mean curvature. The approach is based on a numerical technique that embeds the evolving hypersurface as the zero level set of a family of evolving surfaces. In this setting, the resulting partial differential equation for the motion of the level set function $\phi$ may be solved by using numerical techniques borrowed from hyperbolic conservation laws. This technique is used to analyze a collection of problems. First we analyze the singularity produced by a dumbbell collapsing under its mean curvature and show that a multi-armed dumbbell develops a separate, residual closed interface at the center after the singularity forms. The level set approach is then used to generate a minimal surface attached to a one-dimensional wire frame in three space dimensions. The minimal surface technique is extended to construct a surface of any prescribed function of the curvature attached to a given bounding frame. Finally, the level set idea is used to study the flow of curves on 2-manifolds under geodesic curvature dependent speed.
Download publications
-
Fast Marching Methods on Triangulated Domains
: Kimmel, R., and Sethian, J.A.,
Proceedings of the National Academy of Sciences, 95, pp. 8341-8435, 1998.
Abstract
The Fast Marching Method is a numerical algorithm for solving the Eikonal equation on a rectangular orthogonal mesh in O(M \log M) steps, where M is the total number of grid points. In this paper we extend the Fast Marching Method to triangulated domains with the same computational complexity. As an application, we provide an optimal time algorithm for computing the geodesic distances and thereby extracting shortest paths on triangulated manifolds.
Download publications
-
The Collapse of a Dumbbell Moving under its Mean
Curvature
: Sethian, J.A., in
Geometric Analysis and Computer Graphics,
P. Concus, R. Finn, D. Hoffman, Eds.,
Mathematical Sciences Research Institute Publications,
Springer-Verlag, 1991,
Abstract
The collapse of a dumbbell moving under its mean curvature has attracted considerable attention. A new class of numerical algorithms have been developed recently that can follow hypersurfaces propagating with curvature-dependent speed in any number of space dimensions. The essential idea behind these algorithms is to view the propagating hypersurface as a particular level set of a higher dimensional function. The motion of this higher-dimensional function is described by a scalar Hamilton-Jacobi equation with parabolic right-hand-side. This equation may be easily solved using techniques borrowed from the solution to hyperbolic conservation laws. We demonstrate this technique applied to the problem of a dumbbell collapsing under its own mean curvature. Our results show the breaking of the handle, the developing singularity, and the collapse of the two separate sections.
Download publications
-
A Computed Example of Nonuniqueness of Mean Curvature
Flow in R^3
: Angenent, S., Ilmanen, T., and Chopp., D.L.,
Comm. Partial Diff. Eqns., 20, 11-1, pp. 1937-1958, 1995.
Download publications
-
Motion by
Intrinsic Laplacian of Curvature
: Chopp, D.L., and Sethian, J.A.,
Interfaces and Free Boundaries, 1, 107--123, 1999.
Abstract
In this paper, we discuss numerical schemes to model the motion of curves and surfaces under the intrinsic Laplacian of curvature. This is an intrinsically difficult problem, due to the lack of a maximum principle and the delicate nature of computing an equation of motion which includes a fourth derivative term. We design and analyze a host of algorithms to try and follow motion under this flow, and discuss the virtues and pitfalls of each. Synthesizing the results of these various algorithms, we provide a technique which is stable and handles very delicate motion in two and three dimensions. We apply this algorithm to problems of surface diffusion flow, which is of value for problems in surface diffusion, metal reflow in semiconductor manufacturing, sintering, and elastic membrane simulations. In addition, we provide examples of the extension of this technique to anistotropic diffusivity and surface enery which results in an anisotropic form of the equation of motion.
Download publications
- Motion of Level Sets by Mean Curvature I : Evans, L.C., and Spruck, J., Journal of Differential Geometry, 33, 635, 1991
- Motion of Level Sets by Mean Curvature II : Evans, L.C., and Spruck, J., Transactions of the American Mathematical Society, 330, 1, pp. 321--332, 1992.
- Motion of Level Sets by Mean Curvature III : Evans, L.C., and Spruck, J., J. Geom. Anal. 2, pp. 121--150, 1992.
-
Motion of Level Sets by Mean Curvature IV
:
Evans, L.C., and Spruck, J.,
J. Geom. Anal., 5, 1, pp.
77--114, 1995.
-
Recent Numerical Algorithms for
Hypersurfaces Moving with Curvature-dependent Speed:
Hamilton-Jacobi Equations and Conservation Laws
: Sethian, J.A.,
Journal of Differential Geometry, 31, pp. 131--161, 1990.