OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
Adaptive Mesh Refinement for Level Set Methods
You are currently in the
topic outlined in red.
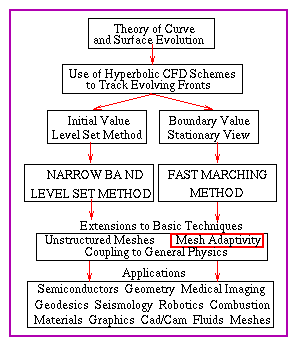
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
Annotated References:
The first work on adaptive mesh refinement in the context of
level set methods was done by Milne in Ref. 1, who did so in his PhD. thesis at
Berkeley.
Milne showed that the handling of the terms associated with the
hyperbolic transport part of the equation of motion was straightforward,
and demonstrated results in two and three space dimensions. In the case
of curvature-driven flow, the techniques are considerably more subtle,
and require a delicate attention to the fine grid/coarse grid boundary.
Unless care is taken, this fine/coarse boundary can act as a source or
sink, and greatly reduce the accuracy of the calculation.
Since this work, a variety of adaptive level set methods have become
available.
- Ref. 2 shows the role of adaptivity in both
level set and Fast Marching Methods.
- Ref. 3 discuss parallel implementation of interface
techniques, including both message-passing architectures and
global programming languages.
New Book and Resource on Level Set and Fast Marching Methods
References:
-
Adaptive Level Set Methods Interfaces
: Milne, B.,
PhD. Thesis, Dept. of Mathematics,
University of California, Berkeley, CA., 1995.
-
Adaptive Fast Marching and Level Set
Methods for Propagating Interfaces
: Sethian, J.A.,
Acta Numerica, Proceedings of
ALGORITMY '97, Zuberec, 1997.
Abstract
Adaptivity provides a way to construct optimal algorithms for tracking
moving interfaces which arise in a wide collection of physical applications.
Here, we summarize the development and interconnection between Narrow Band
Level Set Methods and Fast Marching Methods, which provide efficient
techniques for tracking fronts. We end with a small collection of examples
to demonstrate the applicability of the techniques.
Download publications
-
Parallel Level Set Methods for Propagating Interfaces on
the Connection Machine
: Sethian, J.A.,
Unpublished manuscript, Thinking Machines Corporation, 1989.
Download publications
Additional References:
-
An adaptive level set approach to incompressible two phase flow
:
Sussman, M., Almgren, A., Bell, J., Colella, P.,
Howell, L., and Welcome, M., 148, 1, pp. 81-124, 1999,
New Book and Resource on Level Set and Fast Marching Methods
Abstract
Adaptivity provides a way to construct optimal algorithms for tracking
moving interfaces which arise in a wide collection of physical applications.
Here, we summarize the development and interconnection between Narrow Band
Level Set Methods and Fast Marching Methods, which provide efficient
techniques for tracking fronts. We end with a small collection of examples
to demonstrate the applicability of the techniques.
Download publications
Adaptivity provides a way to construct optimal algorithms for tracking moving interfaces which arise in a wide collection of physical applications. Here, we summarize the development and interconnection between Narrow Band Level Set Methods and Fast Marching Methods, which provide efficient techniques for tracking fronts. We end with a small collection of examples to demonstrate the applicability of the techniques.