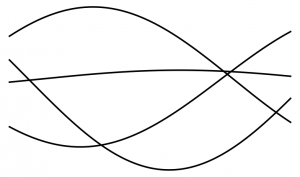
Chamber decomposition of $\mathrm{GL}_n^{\mathit{rss}}/\mathrm{GL}_n$.  Let $\mathbf{z}$ be an $n$-element subset of $\mathbf{C}^*$, e.g. the eigenvalues of a regular semisimple matrix.  For generic $\mathbf{z}$, associate a reduced word decomposition of the long element $w_0 \in S_n$, in the following way.  Each element $z_k \in \mathbf{z}$ determines a stretched-and-shifted cosine graph, $\mathrm{Re}(z_k \exp(i\theta))$ over $\theta \in [0,\pi]$.  The union of these graphs is a positive braid whose projection to $S_n$ is $w_0$.

Here is an example with $n = 4$, very close to a “wall”:

Call this picture $\Phi(\mathbf{z})$ (or maybe better to call it $\Phi(\mathbf{z},[0,\pi])$).  The associated reduced word decomposition is $s_2 s_1 s_3 s_2 s_3 s_1$.   $\mathbf{z}$ lies on a wall exactly when $3$ of the points of $\mathbf{z} \subset \mathbf{\mathbf{C}}^* \subset \mathbf{R}^2$ are collinear.

 

Jimbo-Miwa-Ueno.  Valerio often discusses the connection

$$\nabla = d – \left(\frac{Z}{t^2} + \frac{F}{t}\right)dt$$

on the $t$-line, where $Z$ and $F$ are constant matrices, $Z$ is regular semisimple, and $F$ is chosen to vary isomonodromically with $Z$.  These were studied in 1981 by JMU, or earlier.  More recently, when $A$ is a finite-dimensional algebra and $Z$ is a Bridgeland stability condition on the abelian category of finite-dimensional $A$-modules, Brideland–Toledano-Laredo write down a connection on $\mathcal{O}_{\mathbf{P}^1}\otimes \mathrm{Hall}(A)$ of this type.

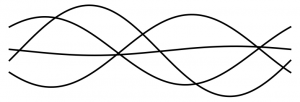
The connection $\nabla$ is regular at $\infty$ and only slightly irregular at $0$.  The Stokes diagram at $0$ is a doubled-up version of the $\Phi$ (attach an upside-down copy of $\Phi(\mathbf{z})$, maybe call the result $\Phi_{[-\pi,\pi]}(\mathbf{z})$)

Thorny character varieties 2.