Let $V$ be a two-dimensional vector space and let $L_0,\ldots,L_{n-1}$ be $n$ lines in $V$ obeying $L_i \neq L_{i+1}$ for all $i \in \mathbf{Z}/n$. Suppose $n$ is odd. If $g \in \mathrm{GL}(V)$ has $gL_0 = L_1,gL_1 = L_2,\ldots,gL_{n-1} = L_0$, then $g^n$ must be a scalar matrix and the ratio of the two eigenvalues of $g$ must belong to $\mu_n – \{1\}$.
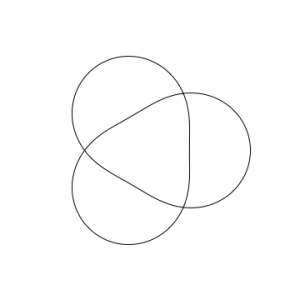
An oriented immersed surface in $\mathbf{R}^3$ determines a Legendrian surface $\Lambda \subset T^{\infty} \mathbf{R}^3 \cong \mathbf{R}^3 \times S^2$ — the projection to the second coordinate is the Gauss map of the immersion. Let $\Sigma_n$ be the “twisted” surface of revolution of the spirograph projection of the $(2,n)$-knot. For example here is $\Sigma_5$:
See it spinning. The set of isomorphism classes of constructible sheaves $F$ on $\mathbf{R}^3$, with the properties
1. $F$ is compactly supported,
2. $F$ has singular support in the Legendrian $\Lambda_n$ lifting $\Sigma_n$,
3. $F$ has microlocal rank one.
is in natural bijection with the set of isomorphism classes of tuples $(L_0,\ldots,L_{n-1},g)$ as above (by a “mapping torus” construction). The microlocal monodromy of $F$ is determined by two scalars: the $\mu\mathrm{mon}$ around the “meridian” is $1$ and around the $\mu\mathrm{mon}$ around the “longitude” (that wraps around the axis of revolution $n$ times) is the eigenvalue of the scalar matrix $g^n$.
There is a funny arithmetic issue. Suppose the ratio of eigenvalues of $g$ is a primitive $d$th root of $1$, say $\zeta_d$, where $d$ is a divisor of $n$ different from $1$. Then the entries of $g$ cannot be taken from any field that does not contain $\zeta_d + \zeta_d^{-1}$. E.g. when $n = 5$ the “field of definition” for any microlocal rank one sheaf with singular support in $\Lambda_5$ must contain $\mathbf{Q}(\sqrt{5})$. In particular, for $n = 5$, there can be no exact filling of $\Lambda_5$. (Not one that is bounded in the base $\mathbf{R}^3$-directions, anyway.) Indeed if $\mathcal{L}$ was such an exact filling, then when decorated with the constant sheaf of $\mathbf{Q}$-modules, Nadler-Zaslow would produce an $F$ that was also defined over $\mathbf{Q}$.
When $d = 3$, $\zeta_d + \zeta_d^{-1}$ is rational, so it is not forbidden that such an $\mathcal{L}$ exists. And indeed the Reeb flow discussed here suggests a way to build $\mathcal{L}$. Without breaking the $\mathbf{Z}/3$-symmetry, we can isotope away the double points of the (2,3) spirograph (trading them for cusps)
Carrying a constructible sheaf on the first figure along this isotopy turns it into a constant sheaf on the interior of the truncated triangle of the last figure, standard on the longer straighter lines and costandard on the shorter curved lines. The twisted surface of revolution looks like this, and it’s hollow inside.
But there is no way to simplify the (2,5) spirograph in a similar way, preserving the $\mathbf{Z}/5$-symmetry. (Here‘s what you get it you try.)


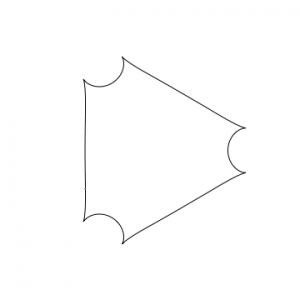
You should 3d print that thing and sell it as jewelry.
Maybe this doesn’t affect your argument anyway, but I didn’t understand why you have g^nL = L. Are you building a sheaf by studying the front projection? And are you looking at what this projection looks like relative to the 2-torus? Are you noticing that the sheets in the cover of the front projection over the 2-torus cross over a locus generated by a (2,n) curve? Then don’t you get g^{n+2}L = L? Or is everything I’m saying wrong?
I don’t understand every question. But if you don’t like $g^n L = L$ and do like $g^{n+2} L = L$, is it because I named the “spirograph projections” differently than you? In this drawing of Harold’s, I would call the top row the (2,3) spirograph projection and the bottom row the (2,5) spirograph projection.
Are you building a sheaf by studying the front projection?
Sort of. Regarding that immersed torus as a front projection of a Legendrian $\Lambda_5 \subset T^{\infty} \mathbf{R}^3$, I am observing that any sheaf on $\mathbf{R}^3$ with $\mathit{SS}^{\infty} \subset \Lambda_5$ must have a weird property, and that weird property forbids the existence of an exact filling.
And are you looking at what this projection looks like relative to the 2-torus?
More like, looking at what it looks like relative to $S^1$. In cylindrical coordinates $r,\theta,z$, (where the $z$-axis goes through the hole of the donut). If you project to the $\theta$-coordinate, the fibers are $(r,z)$-planes, each of which has a spirograph drawn in it (centered at $r = 2$, $z = 0$ or so, say). So in some sense this picture is the mapping torus of the generator of the $\mathbf{Z}/5$-action.
Are you noticing that the sheets in the cover of the front projection over the 2-torus cross over a locus generated by a (2,n) curve?
I agree that the self-crossing locus is a (2,5) torus knot in $\mathbf{R}^3$. I’m sure that’s not a coincidence but it’s not something I used. (I didn’t mean to use it at least.)
Sorry, this takes a video chat for me at the least. Ah, it’s times like these when I regret not being in Berkeley. However, in two days I will be flying to New Zealand, where I should be free from regrets.
Seriously, though, I have never found a good way to view the Gauss map to $S^2$, or more seriously the front projection to $S^2\times\mathbb R$ for a $(2,n)$ curve embedded in ${\mathbb R}^3.$ (Bitangent loci are hard to compute.) Do you crack this nut or make an assumption that the image looks like your spirograph? When I compute, I generally have cusps *unless* I just look at the image relative to $J^1$ of the unknot conormal — but this is not the true sheaf setting.