Theorem. (Nadler-Zaslow) Let $L \subset T^* M$ be an exact Lagrangians, whose brane obstructions are trivial, and that is subject to certain tameness conditions. Then there is a functor from local systems of $\mathbf{C}$-vector spaces on $L$ to constructible sheaves on $M$.
The functor is well-defined up to a shift and signs, coming from the grading and relative pinning, i.e. up to the data of a trivialization of the trivializable brane obstruction. Though the domain and codomain of the functor are sheaf-theoretic, the definition is Floer-theoretic. I’ll sketch a sheaf-theoretic alternative. The main ideas are in Tamarkin and Guillermou, but it will require some extra effort because we are interested in noncompact Lagrangians.
Tamarkin’s cone trick. (Dima does great things with it, I don’t mean to call it a trick.) Let $\Omega$ be the open subset of $T^* \mathbf{R}$ given by pairs $(t,\tau)$ — $t$ is the coordinate on $\mathbf{R}$ and $\tau$ is the covector — with $\tau > 0$. $T^* M \times \Omega$ is naturally identified with an open subset of $T^* (M \times \mathbf{R})$.
For any closed set $L \subset T^* M$, define $\mathrm{Cone}(L) \subset T^* M \times \Omega$ by
$$\mathrm{Cone}(L) = \{(x,\xi,t,\tau) \mid (x,\xi/\tau) \in L\}$$
Then $\mathrm{Cone}(L) \cup$ (zero section) is a closed, conic subset of $T^* (M \times \mathbf{R})$.
If $L$ is smooth, then $\mathrm{Cone}(L)$ is smooth. If $L$ is coisotropic, then $\mathrm{Cone}(L)$ is coisotropic. But $\mathrm{Cone}(L)$ is never Lagrangian. Its dimension is too big, by one.
In fact $\mathrm{Cone}(L) \cong (L \times \mathbf{R}_{>0}) \times \mathbf{R}$. We wish that the $(L \times \mathbf{R}_{>0})$-factor were a Lagrangian in $T^* M \times \Omega$. The second $\mathbf{R}$-factor is Tamarkin’s version of the Novikov parameter.
Exact Lagrangians. There is a $\mathbf{R}_{>0}$-equivariant projection
$$\mathrm{Cone}(L) \to L \times \mathbf{R}_{>0}$$
sending $(x,\xi,t,\tau)$ to $(x,\xi/\tau,\tau)$. A $\mathbf{R}_{>0}$-equivariant section of it is determined by a function $f:L \to \mathbf{R}$. The section is
$$(x,\xi,\tau) \mapsto (x,\tau\cdot\xi,f(x,\xi),\tau)$$
If $L$ is Lagrangian, then the image of this section is Lagrangian if and only if $df = \alpha\vert_L$, where $\alpha$ is the canonical one-form on $T^* M$. In particular $L$ must be exact.
Let’s denote the image of this section — the “Lagrangian cone over an exact Lagrangian” — by $\mathrm{ExCone}(L)$. We suppress $f$ since it is determined up to an additive constant when $L$ is connected. The union of $\mathrm{ExCone}(L)$ with the zero section is a closed [oops] conic Lagrangian in $T^* (M \times \mathbf{R})$. Let’s denote its boundary at contact infinity (a subset of $T^{\infty,+}(M \times \mathbf{R})$ by $\mathrm{ExCone}^{\infty}(L)$. It is diffeomorphic to $L$.
Tameness. In what follows, the Nadler-Zaslow condition that $L$ is tame can be replaced by the condition that $\mathrm{ExCone}(L)$ is contained in the conormal variety of a Whitney stratification of $M \times \mathbf{R}$, that can be extended to a finite Whitney stratification of $M \times [-\infty,\infty]$. (Is it OK if I admit this is a relief to me, since I still do not really understand the role of tameness in NZ?)
Microlocal monodromy and middle pushforward. Let $L$ be an exact Lagrangian filling of $\Lambda \subset T^{\infty} M$. The pure-sheaf-theory Nadler-Zaslow functor will be a pair of functors
$$\mathit{Loc}(\Lambda) \leftarrow \mathit{Sh}_{\mathrm{ExCone}^{\infty}(L)}(M \times \mathbf{R}) \to \mathit{Sh}_{\Lambda}(M)$$
Both functors will kill local systems on $M \times \mathbf{R}$.
The left functor is microlocal monodromy. Defining it is basically the same as “trivializing the brane obstructions”, but whenever it is defined it should be an equivalence. More on that later.
The right functor is easy to define. Start with a sheaf on $M \times \mathbf{R}$ with $\mathit{SS}^{\infty} \subset \mathrm{ExCone}^{\infty}(L)$. Consider the embedding $M \times \mathbf{R} \to M \times [-\infty,\infty]$. Take the $!$-extension along $M \times \{-\infty\}$ and the $*$-extension along $M \times \{+\infty\}$, and the pushforward along the projection $M \times [-\infty,\infty] \to M$.
Example. An exact Lagrangian surface in $\mathbf{R}^4$ determines a Legendrian $\mathrm{ExCone}^{\infty}$ whose front projection is an immersed surface in $\mathbf{R}^3$. We can visualize some exact surfaces of interest, for example here is the graph of $\pm \sqrt{z}dz$
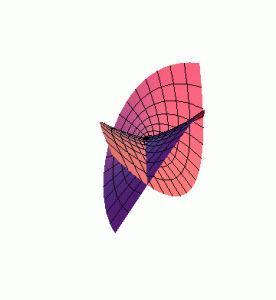
This is great.
It is not automatic that $\mathrm{ExCone}(L) \cup$ zero section is closed. It requires something like: if $(x_i,\xi_i) \in L$ have $\xi_i$ going off to infinity, then $f(x_i,\xi_i)$ also goes off to infinity. For example a Schmid-Vilonen Lagrangian over an open set obeys this, but a cotangent fiber does not.
This condition is havoc at cusps.
Looks super cool! Minor typo, mostly to make sure I understood the content enough to accurately locate it: the first sentence of “Exact Lagrangians” should be “…sending ((x,ξ,t,τ) to (x,ξ/τ,τ)…” rather than “…sending (x,ξ,t,τ) to (x,ξ/τ,t)…” right? (i.e. a t and τ are swapped)
I convince myself this really is the same as NZ by working out the details for standard sheaves, right?
You are right about the typo.
I convince myself this really is the same as NZ by working out the details for standard sheaves, right?
You will see that the construction turns a standard (Schmid-Vilonen) Lagrangian into a standard sheaf. But I don’t see how to deduce what happens for general Lagrangians from what happens for standard ones: for that, the fact that they generate the Fukaya category is not so useful.
Random quasi-related topic: suppose I have a Lagrangian in $T^*M$ which is not exact but bounds no J-holomorphic disks. My impression was that such a thing should in some sense be as good as an exact Lagrangian as far as microlocalization is concerned — is that basically correct? It looks less so in this construction. I raise the issue because a discussion with Andy the other day led to the conclusion that a generic spectral curve *should* have this property (I think he is going to write this up on the blog soon).
My understanding (just from being told so) is: if $L$ bounds no holomorphic disks, or else is “monotone”, then the Floer-theoretic analog of Nadler-Zaslow will make sense over the Novikov ring. And Andy has mentioned before (maybe in a different context, that we are hoping is isomorphic?) that when there is wild ramification somewhere then all the Novikov series that arise should converge.
Maybe we could understood Tamarkin’s trick well enough to tell the same story without Floer theory. I have a good feeling about it, but nothing more concrete than that.
If $L$ is the graph of $df$ in $T^*M$ then $ExCone^\infty(L)$ is the graph of $J^1(f)$ in $J^1(M)\cong \left\{\tau=1\right\}\subset T^*(M\times \mathbb R.$ Does this observation help relate this construction to Vivek’s gfacs?
Hi David,
This is great! It seems to me that the construction of the Lagrangian cone is very similar to the inverse process of taking the Lagrangian projection of a Legendrian in $T^*M\times\mathbb{R}$ (with the standard contact form $dz+\lambda_{can}$), and then taking the cone over the Legendrian in the symplectization of the contact manifold. Of course, the usual symplectization of $T^*M\times\mathbb{R}$ is not the same as $T^*(M\times\mathbb{R})$ with its standard symplectic structure, and the conical structure is just on the cotangent fibers of $T^*\mathbb{R}$. One can modify this construction to some other symplectizations of $T^*M\times\mathbb{R}$, including $T^*(M\times\mathbb{R})$ with its standard symplectic structure, as long as there is a compactible $J$ sending the conical direction that one chooses to the Reeb vector field, and at the end one takes the cone over the Legendrian with respect to the conical structure (and may need to union with the zero section in the case you described).
So from this point of view, Legendrian contact homology for $T^*X\times \mathbb{R}$ is something close to the Floer homology (include counting holomorphic polygons) of immersed Lagrangians in $T^*X$ (which are their projections). One evidence for this is in the paper by Etnyre-Ng-Sabloff, where counting holomorphic polygons for the LCH of Legendrian knots in $\mathbb{R}^3$ is the same as counting immersed discs in $\mathbb{R}^2$ bounded by their Lagrangian projections. Similarly, one would hope that Legendrian contact homology for multiple Legendrians is close to calculating morphisms for a sequence of branes in $T^*X$. These are just heuristic guesses, whose proof/disproof would rely on a lot of analysis. I guess what you are saying is that $Sh_{ExCone(L)^\infty}(M\times\mathbb{R})$ is something equivalent to these without appealing to holomorphic discs.
I would also like to understand what happens with an immersed $L$. Are you suggesting that if we take for our immersed $L$, the union of several embedded $L_1$, $L_2$, … we should be able to compute $HF(L_1,L_2,..)$ from sheaves with singular support in $\mathrm{ExCone}^{\infty}(L)$? I’m not sure it works when $L$ is the union of two standard branes in $T^* \mathbf{R}$.
I would prefer a single immersed $L$ to be connected after a smooth Legendrian lifting. If $L=\cup L_i$, then a lifting would be of several components, and I imagine the LCH calculates some of the $A_\infty$-compositions in the Fukaya category involving $L_1,L_2,…$ (not necessarily all of them, which depend on the lifting). I don’t have a very satisfying answer to what sheaf can tell about this. Maybe one point is there is no canonical lifting of the Lagrangians, so when they are translated independently in the $t$-direction, they will give different sheaf categories. For example, if $L=L_1\cup L_2$ and $\bar{L_1}\cap \bar{L_2}=\emptyset$, then $Sh_{ExCone^\infty(L)}$ will always stay the same regardless of how $ExCone^\infty(L_1)$ and $ExCone^\infty(L_2)$ are moving. However, if $L_1$ and $L_2$ intersect, then there will be something interesting happening. This is like detecting how the moves of the liftings are far from non-characteristic, but I am not sure whether there is a right formalism for it.
Hi Xin. I wonder what you make of this class of immersed examples:
If you start with an exact, compact, connected, immersed Lagrangian $L$ in $T^* S^1$, the diagram
$$\mathit{Loc}(L) \leftarrow \mathit{Sh}_{\mathrm{ExCone}^{\infty}(L)}(S^1 \times \mathbf{R}) \to \mathit{Sh}_{\Lambda}(S^1)$$
makes sense, but the left arrow is not an equivalence.
As $L$ is compact, $\Lambda$ is empty and the category at the right is $\mathit{Loc}(S^1)$. The front projection of $\mathrm{ExCone}^{\infty}(L)$ is what we called a cylindrical braid closure, $\beta^{\circ}$ in STZ. The middle category is $\mathcal{C}(\beta^{\circ})$, it and the map to $\mathit{Loc}(S^1)$ are related to Bott-Samelson and HOMFLY in STZ section 6.
As a map of moduli spaces, the left map is a bundle with affine-space fibers. I wonder whether to expect that in general?
Hi David,
There are two things that I don’t quite understand. First, if $L$ is embedded, then you say the arrows in the above diagrams are all equivalences. But I don’t see local systems on $M\times\mathbb{R}$ from $Loc(L)$? The other question is why the left arrow is an equivalence or not depends on whether $L$ is embedded. You mentioned something like brane obstruction, but I don’t get it. Could you help me with these?
Another thing that is tempting to me is that one might be able to calculate Floer cohomology (or even the $A_\infty$-structures) from the categories $Sh_{ExCone^\infty(L)}(M\times\mathbb{R})$. For example, if $L=L_1\cup L_2$, then there are different liftings of $L$, and I imagine the difference of the corresponding sheaf categories characterizes their Floer cohomologies. More precisely, for $Hom(L_1,L_2)$, one fixes Legendrian liftings $\tilde{L}_1$, $\tilde{L_2}$, and then one compares the categories $Sh_{\tilde{L}_1^{-s}\cup\tilde{L_2}}(M\times\mathbb{R})$ with $Sh_{\tilde{L}_1^{s}\cup\tilde{L_2}}(M\times\mathbb{R})$ for $s\rightarrow+\infty$, where $\tilde{L_1}^{s}$ means translating $\tilde{L_1}$ in the $t$-direction by $s$. The reason for this is that the characteristic moves of the Legendrians correspond to the intersections of the underlying branes.
Here are two pictures (pic1, pic2) for $L_1$=a standard brane over an open interval and $L_2=$the zero section in $T^*\mathbb{R}$. In the first picture, I try to write down the different categories, in terms of restriction maps of local sections by the microlocal conditions, but I am not sure whether I get the full characterizations (e.g. the top one and the last one in the first picture), and I wonder whether you have some insights in how to compare the categories (taking quotients?). The second picture is to illustrate that the calculation should be invariant under any bending of the branes, i.e. the holomorphic discs should kill some of the differences caused by each step of characteristic moves.
First, if L is embedded, then you say the arrows in the above diagrams are all equivalences
I was wrong. In fact this is not true even in cases that are of great interest to us, such as when $M = \mathbf{C}^*$ and $L$ is the graph of $\pm dz/\sqrt{z}$. (Here is an animation of the front projection of $\mathrm{ExCone}^{\infty}(L)$. Note as in this example, the double points lie above the walls of a spectral network) Restricting our attention to moduli spaces, the diagram
$$
\mathit{Loc}(L) \leftarrow \mathit{Sh}_{\mathrm{ExCone}^{\infty}(L)}(M \times \mathbf{R}) \rightarrow \mathit{Loc}(M)
$$
becomes
$$
\frac{\mathrm{GL}_1}{\mathrm{GL}_1} \leftarrow \mathcal{M} \rightarrow \frac{\mathrm{GL}_2}{\mathrm{GL}_2}
$$
where $\mathcal{M}$ is the quotient of $\{(g,x) \in \mathrm{GL}_2 \times \mathbf{P}^1 \mid gx \neq x\}$ by $\mathrm{GL}_2$. The right map sends $(g,x)$ to $g$ while the left map sends $(g,x)$ to $-\mathrm{det}(g)$.
Your guess is as good as mine! What does the official Nadler-Zaslow construction do to a local system on $\pm dz/\sqrt{z}$, different from the trivial local system?
In the first picture, I try to write down the different categories, in terms of restriction maps of local sections by the microlocal conditions, but I am not sure whether I get the full characterizations (e.g. the top one and the last one in the first picture), and I wonder whether you have some insights in how to compare the categories (taking quotients?).
Another time that your guess is as good as mine. I think you have all categories correct. To “take quotients”, you can just put $W = 0$. It looks like there are specialization functors from the categories in the first or second row, the the category in the third row. Are those functors geometrically meaningful?
I was wrong.
I think it should be OK, if $L$ has compact horizontal support, and does not have any self-intersection points at infinity.
Thanks David!
Have you checked that $\sqrt{z}dz$ (with the trivial local system) corresponds to the trivial rank two sheaf using your equivalences?
Actually, I miss some points in your claim and your remark on $dz/\sqrt{z}$. For $Loc(M)$, why is it $\frac{GL_2}{GL_2}$? In other words, why do we only consider rank two local systems here? I guess one could always compactify the base manifold (and then the branes), say from $\mathbb{C}^*$ to $\mathbb{P}^1$, are there any essential differences for your claim?
Yes, a rank one local system on $\sqrt{z}dz$ gives the trivial rank two local system on $\mathbf{C}$.
$\mathrm{ExCone}(dz/\sqrt{z})$ is closed in $T^*(\mathbf{C}^* \times \mathbf{R})$, but it is not closed in $T^*(\mathbf{P}^1 \times \mathbf{R})$. I haven’t worked it out carefully, but I think if you perturb $dz/\sqrt{z}$ slightly in $T^* \mathbf{P}^1$ and then take $\mathrm{ExCone}$, it will be closed and will produce a constructible sheaf on $M = \mathbf{P}^1$ more complicated than a local system (with knots around the punctures).
What do cobordisms do?
More precisely: Hiro Tanaka + David Nadler have some construction of a category with objects exact lagrangians, morphisms something built out of cobordisms, which they map to the Fukaya category. Presumably, it makes as much sense, if maybe not more, to map the Tanaka-Nadler category to the category you describe here….
Which category do you want to map their cobordism category to?
Hi David,
Based on your comment about specializations, I think the following categorical calculations of Floer cohomology (and higher $A_\infty$-structures) should work, though there are some parts I’m not quite sure. Before describing this, some (easy) comments are: when we look at the projection of the Legendrian lifting of a Lagrangian graph $L_{df}$ in $T^*M$ to $M\times \mathbb{R}$, it is just the graph of $f$ in $M\times\mathbb{R}$; when we have two Lagrangian graphs $L_{df_1}$ and $L_{df_2}$, and consider the projection of $\tilde{L}_{df_1}^{s}\cup\tilde{L}_{df_2}$ for $s\in\mathbb{R}$, the moments when critical behavior happens are corresponding to $s\in CritVal(f_2-f_1)$, so in particular there are only differentials from large $s$ to some $s$ (note that the grading for Floer cohomology is opposite to Morse homology). Essentially we are doing Morse theory, and we wanted some algebraic framework (avoiding holomorphic discs) of this to extend to arbitrary Lagrangians, which can be thought as generalized Morse theory.
Given any two (exact) Lagrangians $L_1,L_2$, consider the infinity of $\bigcup\limits_{s\in\mathbb{R}}(ExCone(L_1)+s;s,-1)\subset T^*(M\times\mathbb{R}\times\mathbb{R})$ with coordinate $(x,\xi; t,\tau; s, \theta)$ ($ExCone(L_1)+s$ means shift the $t$-coordinate of $ExCone(L_1)$ by $s$) and $ExCone(L_2)\times\mathbb{R}\times\{0\}\subset T^*(M\times\mathbb{R}\times\mathbb{R})$, and denote these two Legendrians by $\Lambda_1$ and $\Lambda_2$ respectively. Consider $Sh_{\Lambda_1\cup\Lambda_2}(M\times\mathbb{R}\times\mathbb{R})$, then this category is clearly invariant under Lagrangian isotopies of $L_1$ and $L_2$ (relative to the infinity). Similarly $\lim\limits_{s\rightarrow\pm\infty}Sh_{\tilde{L}_1^{s}\cup \tilde{L}_2}(M\times\mathbb{R})$ is invariant under Lagrangian isotopies. There are restriction functors $\rho_{\pm\infty}$ from $Sh_{\Lambda_1\cup\Lambda_2}(M\times\mathbb{R}\times\mathbb{R})$ to $\lim\limits_{s\rightarrow\pm\infty} Sh_{\tilde{L}_1^{s}\cup \tilde{L}_2} (M\times\mathbb{R})$ respectively. The proposed “categorical” Floer cohomology $\mathcal{HF}(L_1,L_2)$ is $Cone(\rho_{-\infty})$ (and $\mathcal{HF}(L_2,L_1)$ should be $Cone(\rho_{+\infty})$). Here is a question that I wonder about.
\textbf{Question}: How to get a graded vector space from taking cone of categories?
Now let $s_1<s_2<…<s_n$ be the critical moments where $\tilde{L}_1^{s}\cap\tilde{L}_2\neq\emptyset$. Let $Sh_{s}$ denote for $Sh_{\tilde{L}_1^{s}\cup \tilde{L}_2} (M\times\mathbb{R})$ and $Sh_{(i)}$ denote for $Sh_{s}$ for any $s_{i}<si$, can be defined as
(**) $Cone (Sh_{(i-1)}\times_{Sh_{s_i}}\cdots\times_{Sh_{s_{j-1}}} Cone(Sh_{(j-1)}\times_{Sh_{s_j}} Sh_{(j)}\rightarrow Sh_{(j-1)})\rightarrow Sh_{(i-1)})$
$$\rightarrow Cone(Sh_{(i-1)}\times_{Sh_{s_i}} Sh_{(i)}\rightarrow Sh_{(i-1)})$$
I am not sure whether this is a good formulation. The meaning of this is illustrated in this example.
There are also similar constructions for (higher) compositions. For example, given $L_0, L_1, L_2$, to compute $Hom(L_1,L_2)\otimes Hom(L_0,L_1)\rightarrow Hom(L_0,L_2)$, one takes $(ExCone(L_0)+s_1+s_2; s_1,-1;s_2,-1)$, $(ExCone(L_1)+s_1;s_1,-1;s_2,0)$ and $ExCone(L_2)\times\mathbb{R}\times\{0\}\times\mathbb{R}\times\{0\}$ in $T^*(M\times\mathbb{R}^3)$ with coordinate $(x,\xi; t,\tau; s_1,\theta_1;s_2,\theta_2)$ and $ExCone(L_0)+s_1+s_2$ means shifting the $t$ coordinate by $s_1+s_2$. Let $\{s_1^{(i)}\}, \{s_2^{(i)}\}$ and $\{s_3^{(i)}\}$ be the set of critical values for the pairs $(\tilde{L}_1, \tilde{L}_2)$, $(\tilde{L}_0, \tilde{L}_1)$ and $(\tilde{L}_0, \tilde{L}_2)$ respectively. Then one draws the hyperplanes for these critical values as in this picture (these divide the $(s_1,s_2)$-plane into regions with different configurations of $(\tilde{L}_0^{s_1+s_2}, \tilde{L}_1^{s_1}, \tilde{L}_2)$. To calculate compositions, one finds all possible triangles like the one in yellow, and finds all possible “Morse trees” as illustrated in blue. The formulation of the composition map is similar as before: along a Morse tree, one can form fiber product of sheaf category, and take appropriate cones. For higher compositions $\mu_n$, one considers $n$-simplices and then the “dual” to them are Morse trees with $n-1$ inputs and 1 output.
If one can show that these give an $A_\infty$-structure, then these would give a purely algebraic description (avoiding counting discs) for $Fuk(T^*M)$. To show $\mu\circ\mu=0$, I guess one needs some moduli description for (**). Do you have any suggestion about that? Thanks!
$(ExCone(L_1)+s;s,-1)$ should be replace by $Cone(ExCone(L_1)\cap \{\tau=1\}+s;s, -1)$, and similarly for other terms like this.
If $L$ is an immersed, exact Lagrangian in $T^*M$ then David’s transform ${\rm ExCone}(L)$ the unique-up-to-Reeb Legendrian lift of $L$. That is, we think of $L$ as living in the Lagrangian projection of $J^1(M) = (T^*M) \times \mathbb R.$ Then the sheaf lives in $M\times \mathbb R.$
This explains the spectral network observation. Take $L$ to be the graph of $Re(\mpi\sqrt{z}dz) = Im(\pm\sqrt{z}dz) Then the height coordinate of David’s pictures is the imaginary part of $\int{\pm\sqrt{z}dz$, which is zero along the real trajectories of the quadratic differential $z(dz)^2,$ i.e. the spectral lines.
If $L$ is an immersed, exact Lagrangian in $T^*M$ then David’s transform ${\rm ExCone}(L)$ the unique-up-to-Reeb Legendrian lift of $L$. That is, we think of $L$ as living in the Lagrangian projection of $J^1(M) = (T^*M) \times \mathbb R.$ Then the sheaf lives in $M\times \mathbb R.$
This explains the spectral network observation. Take $L$ to be the graph of $Re(\mp i\sqrt{z}dz) = Im(\pm\sqrt{z}dz).$ Then the height coordinate of David’s pictures is the imaginary part of $\int{\pm\sqrt{z}dz$, which is zero along the real trajectories of the quadratic differential $z(dz)^2,$ i.e. the spectral lines.
——
p.s. I can’t edit prior comments/posts anymore!
I don’t know why some sentences have been deleted in my comment after being pending for some time. Maybe it is too long to be a comment. I will turn it into a post.