Let $M$ be a one-dimensional manifold.  A thorn on $M$ is a ray in $T^{\ast }M$, or equivalently a point of $T^{\mathrm{\infty }}M$.

Thorns $S\subset T^{\mathrm{\infty }}M$ are in “general position” if the projection $\pi :S\to M$ is injective.  If $S$ is in general position then we define a quiver $Q_S$:

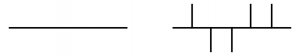
1.  The vertices of $Q_S$ are the bounded components of $M–\pi (S)$.  (We can negotiate whether to include the unbounded components.)

2.  The edges of $Q_S$ are the thorns, with $s$ connecting $v$ to $w$ if $v\cup \{\pi (s)\}\cup w$ is connected.

3.  Orient $s:v\to w$ if $s$ takes negative (sorry) values on the vector at the boundary of $v$ that points toward $w$.

For example with $M$ and $S$ as in the figure above, $Q_S$ is given by $\bullet \to \bullet \to \bullet \leftarrow \bullet$.  In general when $M$ is homeomorphic to $\mathbf{R}$, $Q_S$ has type $A_{n-1}$ where $n$ is the number of thorns.  If $M\cong S^1$, then $Q_S$ has affine type $A_{n-1}$ where $n$ is the number of thorns.

When $S$ is in general position, the derived category of sheaves on $M$ with singular support in $S$ is equivalent to the derived category of representations of the quiver $Q_S$. Under this equivalence, the microlocal stalk at the thorn $s$ is the cone on the map corresponding to the edge corresponding to $s$.

 

Bernstein-Gelfand-Ponomaraev construct equivalences between derived representation categories of two different orientations of a quiver.  This could partly, not entirely, be deduced from GKS.  These equivalences do not respect the $t$-structures.

 

If $M$ is a circle and there are $n=p+q$ thorns — $p$ in one component and $q$ in another component of $T^{\mathrm{\infty }}M$ — a Beilinson-Bondal equivalence identifies ${\mathit{Sh}}_S(M)$ with the derived category of coherent sheaves on a weighted ${\mathbf{P}}^1$.  Weighted means there is one ${\mu }_p$-orbifold point and one ${\mu }_q$-orbifold point.

 

For a quiver $Q$ it is a good idea to fix a dimension vector $\overrightarrow{d}$ and study $\mathrm{Rep}(Q,\overrightarrow{d})/\mathrm{GL}(\overrightarrow{d})$, which parametrizes objects in the heart of the $t$-structure and in a fixed $K$-theory class.  The numerator is a vector space and if $Q$ is of finite ADE type, the denominator acts with finitely many orbits.  If $Q$ has affine ADE type, the denominator acts with one-parameter families of orbits, with a distinguished finite number of them called “nilpotent orbits” by Lusztig.  (Under Beilinson-Bondal, these are the ones set-theoretically supported at the two orbifold points.)

 

The categories of sheaves on $\mathrm{Rep}(Q)$ (sheaves on sheaves…) are related for different orientations of $Q$, and in the finite case Lusztig shows the set of $IC$ sheaves are preserved by these relations.  Lusztig’s argument reminds me of ruling filtrations.

 

Our experience with Legendrian knots (but these are more like links) says to fix a potential $p:S\to \mathbf{Z}$ and study those constructible sheaves for which ${\mu }_s(F)\cong \mathbf{C}[p(s)]$.  If $p$ is $\{0,1\}$-valued, and obeys a Dyck condition, then these $F$ are in the heart of the $t$-structure.  The dimension vector is of the form $1212321$ or something like that.  The thorny character variety for this potential is the open orbit in $\mathrm{Rep}(Q,\overrightarrow{d})$.

 

The cotangent structure on $T^{\ast }\mathbf{R}$ obscures the rotational symmetry of its Fukaya category. Kontsevich has given a description of the stability manifold of representations of the $A_n$ quiver — it is the space of quadratic differentials of the form

$$e^{f(z)}d{z}^{2}f(z)=z^{n+1}+a_1{z}^{n-1}+a_2{z}^{n-2}+\cdots +a_n$$

modulo the action of $(n+1)$st roots of unity on $z$. Note $f(z)$ and $f(z)+2\pi i$ give the same $e^{f(z)}$. The exponent is the unfolding of the type $A$ singularity $z^{n+1}=0$.

Each such quadratic differential gives a flat metric $|e^{f(z)}|(d{x}^2+d{y}^2)$ on $\mathbf{C}$. This metric is not complete, its completion is obtained by adding $(n+1)$ points on the boundary (thorns). Some pairs of these points can be joined by geodesics, which are special Lagrangians that generate the Fukaya category. Integrating $e^{f(z)}dz$ against them (an oscillatory integral, like the Airy function) gives the central charge.

 

Last week Xin pointed out that flat coordinates for this metric are given by the real and imaginary parts of $\int e^{f(z)/2}dz$.