Let $S$ be a surface, let $\Lambda = \{\lambda_i\}_{i \in I}$ be a Legendrian link in $T^{\infty} S$ with components $\lambda_i$. Write $\phi_i \subset S$ for the front projection of $\lambda_i$. Write $\underline{\Lambda} \subset T^* S$ for the conic Lagrangian obtained by coning off $\Lambda$ and taking the union with the zero section.
Let $M$ be the result of attaching a Weinstein handle to each $\lambda_i$. Then $M$ has a skeleton $\mathit{Sk}(M)$ obtained by attaching a disk to each $\phi_i$, or equivalently by taking $\underline{\Lambda}$, compactifying with the $\Lambda \subset T^{\infty}$, and then contracting each $\lambda_i$ to a point.
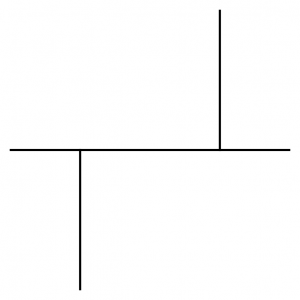
We might regard $\mathit{Sk}(M) \subset M$ as an analog of a ribbon graph $\Gamma$ in an open surface. An open surface has a unique symplectic structure with infinite area around the punctures, and any ribbon graph will be a Lagrangian skeleton. The combinatorial types of ribbon graphs index the cells in a cell complex that is a model for the Teichmuller space of the surface. The top-dimensional cells are trivalent ribbon graphs, and a path through a codimension one cell looks like
(the “edge move”). The Fukaya category is the category of representations of an $A_3$-quiver with different orientations, equivalently the category of constructible sheaves on a line, as the picture is $C^0$-symplectomorphic to a family of conic Lagrangians in $T^* \mathbf{R}$:
Under the identification with representations of $\bullet \leftarrow \bullet \rightarrow \bullet$ and $\bullet \rightarrow \bullet \leftarrow \bullet$ (more here), the equivalence of categories is a BGP functor.
We wish to tell an analogous story for $M$ and its skeleta. If each $\phi_i$ is the oriented conormal of an embedded curve $\phi_i \subset S$, and any two such embedded curves intersect transversely, then $\mathit{Sk}(M)$ labels a top-dimensional cell in the space of skeleta: it has arboreal singularities. (Of type $A_2 \times I$ along the smooth parts of the curves $\phi_i$, and of type $A_3$ where $\phi_i$ and $\phi_j$ intersect.) We seek a disk move to match the edge move one dimension down: a way to contract a disk to a point and expand it again to a skeleton in an adjacent cell.
A standard model for this comes from the focus-focus fibration $\mathbf{C}^2 \to \mathbf{C}$:
$$\mathit{FF}_c = \text{fiber over $c$} \cup \text{Lefschetz thimble over an interval from $c$ to $0$}$$
where $c$ is a real constant. At $c = 0$, this fiber is the union of two Lagrangian planes meeting transversely (the “thimble” is just the double point). At $c \neq 0$, the thimble is the disk being contracted and the fiber is a Lagrangian cylinder (an exact one, as $c$ is real).
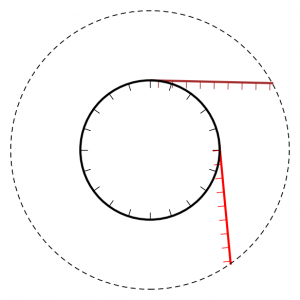
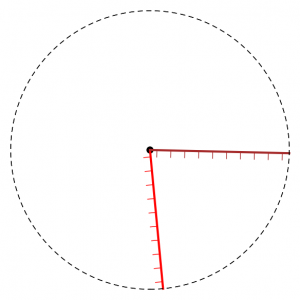
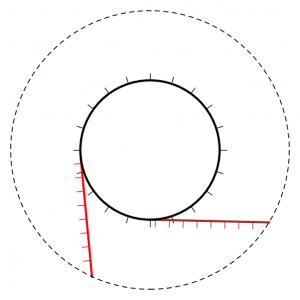
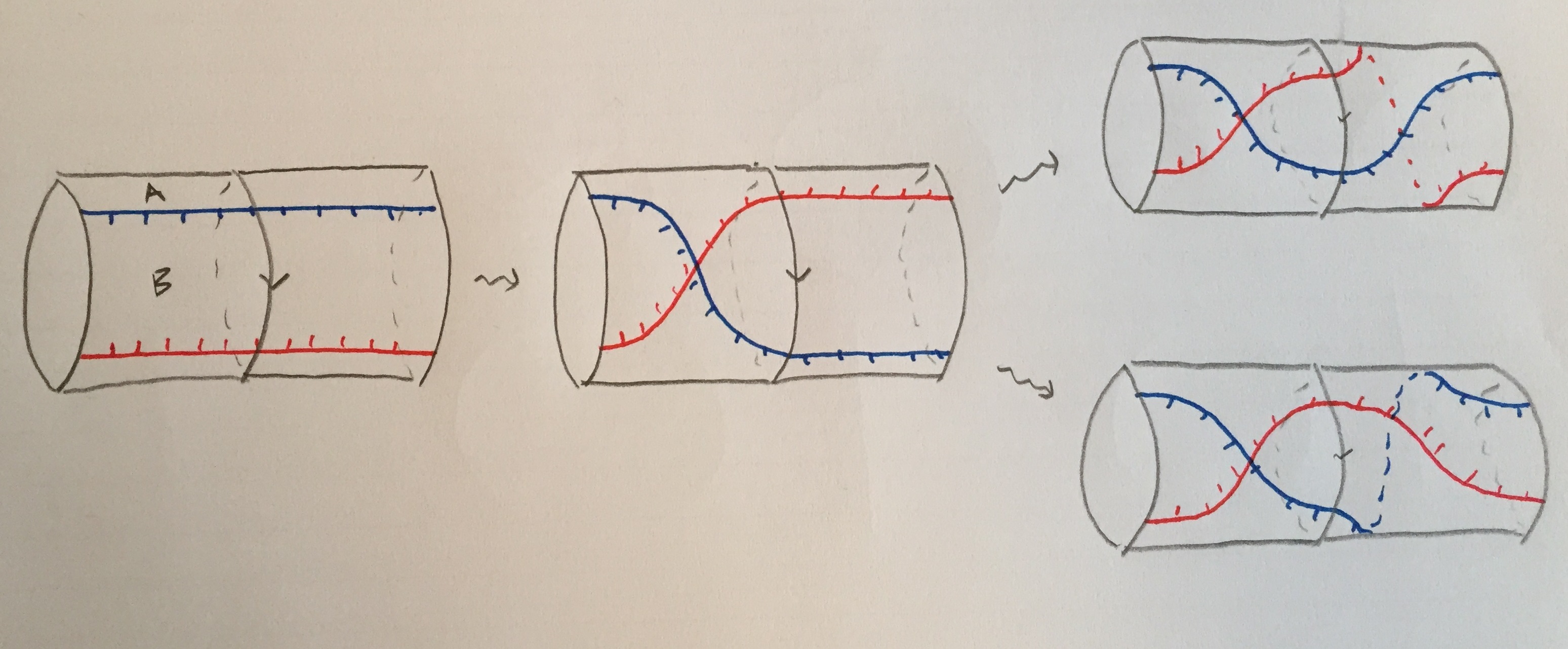
For $c < 0$, if we wish to identify $\mathit{FF}_c$ with an open set $U \subset \mathit{Sk}(M)$ containing the disk $D_i$, the picture is incomplete. The other disks $D_j$ enter $U$ wherever $\phi_j$ crosses $\phi_i$, attaching a Lagrangian fin to $\mathit{FF}_c$. It can probably be added to $\mathit{FF}$ in a compelling way, but instead here is a conic model of the whole thing in side of a cotangent bundle of $\mathbf{R}^2$:
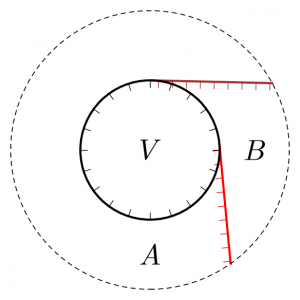
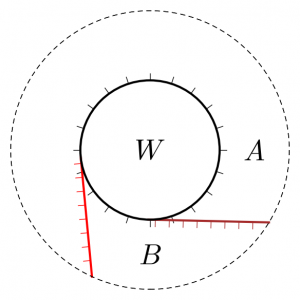
Each figure indicates a conic Lagrangian in $T^* \mathbf{R}^2$. In the left figure, $D_i$ is the disk enclosed by the solid circle decorated with inward-facing conormals. Those conormals together with the remainder of $\mathbf{R}^2$ make the surface $S \cap U$, and the brown- and red- conormals illustrate a pair of nonempty $D_j \cap U$. (The crossing $\phi_i \cap \phi_j$ is the point of tangency the brown or red line makes with the black circle). In the middle figure, the disk $D_i$ has been contracted to a point and $S$ has become nodal, its two branches being $\mathbf{R}^2$ and the cotangent space to the black dot at the origin. In the right figure the disk has been expanded again, now with outward-facing conormals.
Each of these conic Lagrangians has an associated category of constructible sheaves on $\mathbf{R}^2$, which can be seen to be equivalent to each other by using the group structure on $\mathbf{R}^2$ and convolving with a standard or costandard sheaf on a disk. The equivalence matches these two sheaves up:
The maps $A \to B \to A$ determine a constructible sheaf on the annulus, and the maps $V \to A$ and $V \to B$ determine a map $V \to \Gamma(\text{annulus}, A \leftrightarrow B)$ — $W$ is the cone on this map.
—————– added 8/2 ————————————
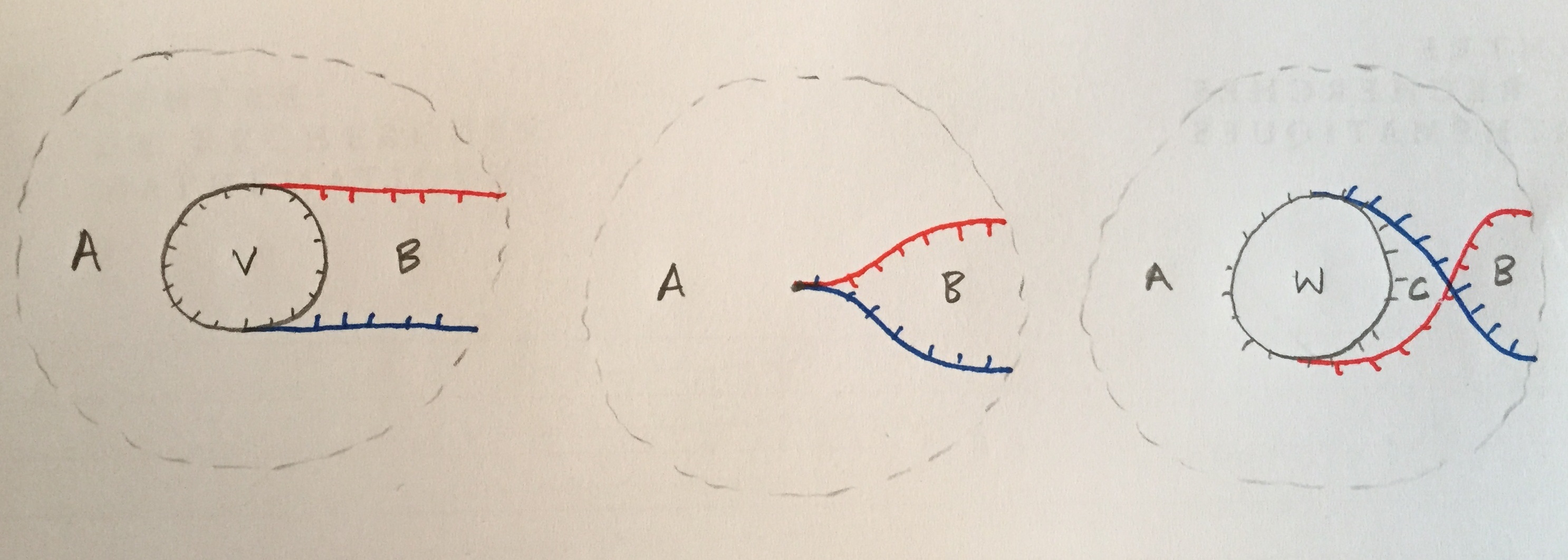
Here’s the picture Vivek requested, and some exposition on how David’s sheaves relate to Vivek’s half-twist:
As before, in the lefthand picture $B \to A \leftarrow B$ is a sheaf $F$ on the annulus $\{1/2< R< 1\} \subset D^2$, and we have a map from $V$ to $\Gamma(F)$. On the right we have a sheaf $G$ on the annulus and a map $\Gamma(G) \to W$.
Let's think about why this is a picture of a cluster transformation. In the lefthand picture the cluster chart consists of sheaves where $F$ is a rank one local system and $V$ is zero. Likewise, in the righthand picture the cluster chart consists of sheaves for which $G$ is a rank one local system and $W$ is zero. What is the intersection of the two cluster charts, as defined by the isotopy isomorphism of the lefthand and righthand moduli spaces? Well, $G$ is a local system when $F$ is, and $W$ is the cone over the map $V \to \Gamma(F)$. This is zero exactly when the holonomy of $F$ around the annulus is not 1, which is exactly what we want. In particular the two charts are glued by a cluster transformation in a general sense where we don't keep track of coordinates, and just ask that the complement of the intersection is where some monomial is equal to 1.
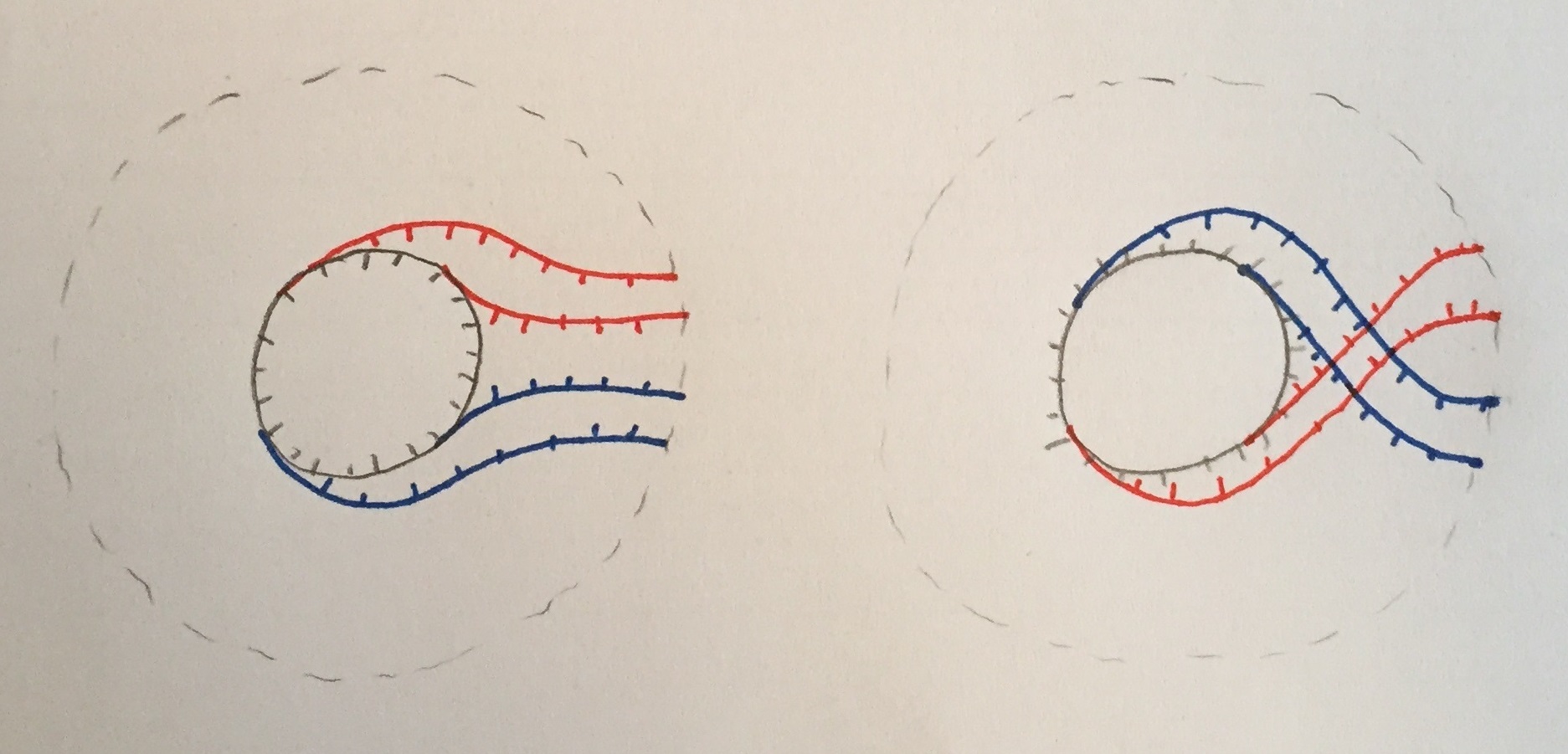
Now let's think about $S$ and $S'$, i.e. the skeleta on either side minus the interiors of all the Lagrangian disks. There is a canonical homeomorphism $S \smallsetminus C \cong S' \smallsetminus C$ which does not extend continuously to $C = \{R = 1/2\} \subset D^2$. This is because $S \smallsetminus C$ and $S' \smallsetminus C$ are both canonically homeomorphic to the union of the annulus $1/2 < R < 1$ and the product of $R_+$ and a cocircle fiber. Since the framing on $C$ is reversed in the right and left pictures this is literally a "half-twist", i.e. the failure to be continuous is exactly by the antipodal map on $C$. If we want to identify $H^1(S)$ and $H^1(S')$ we have to make a choice of isotopy from the half-twist to a homeomorphism $S \smallsetminus C \cong S' \smallsetminus C$ that extends to a homeomorphism $S \cong S'$. There are two ways of doing this: one way it looks like we leave the blue curve alone and the red now winds around $C$, the other way it looks like we leave the red curve alone and the blue curve gets wrapped around $C$ with the opposite orientation. In particular they differ by a Dehn twist around $C$:
The case of arbitrary numbers of curves with arbitrary intersection numbers is essentially just more bookkeeping, see for example:
Note that this description of the surgery keeps track of the mutant disks in Vivek’s desired sense, since they just get carried through the isotopy as the cones over the red and blue strands (more precisely, the red and blue parts of the Legendrian pictured here cut off corners of the corresponding disks, and these corners appear here as conical Lagrangians. These corners get carried through the isotopy and we can glue them back the rest of the disk after doing the local calculation). I think we now basically have a sheaf-theoretic proof that $\mathcal{M}(\Lambda)$ and its generalization to arbitrary cluster types (we should reflect on the ideal notation for this) contain all cluster charts. Question: can we extract from the sheaf theory geometric statements about exact fillings? I.e. can we turn the above into an embedded picture?
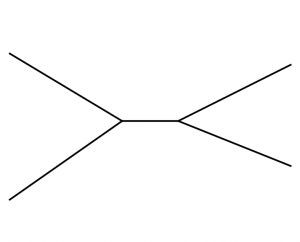
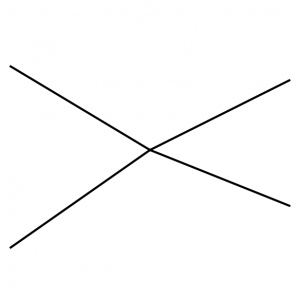
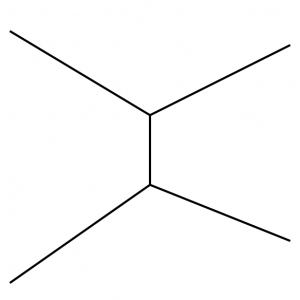
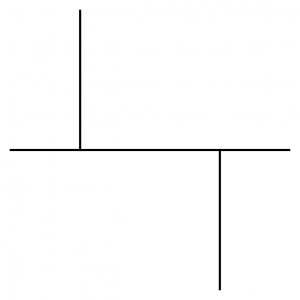
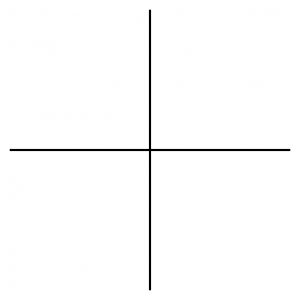
The existence and abundance of infinite type cluster algebras, suggest that unlike the space of 1d ribbon graphs, the space of 2d ribbon graphs has infinite type. A “codimension two cell” (labeled by a more-singular-than-nodal Lagrangian surface) might be adjacent to infinitely many top-dimensional cells (labeled by Lags with arboreal singularities).
Can you remind me of the formula for the focus focus fibration, and the symplectic structure in which the fibres are Lagrangian?
Can you draw the picture of what happens when the red and brown Lagrangians have hairs facing the opposite ways from each other? (I believe the answer should be “not in the same way”, since what has to happen in this case is that the curves along which they meet the cylinder are supposed to intersect after the transition, since that’s what a mutation does.)