Let $\Phi(p,q)$ be a rainbow-style front projection of the Legendrian $(p,q)$-torus knot.  Let $\mathcal{M}_1(p,q)$ be its moduli of constructible sheaves of microlocal rank one.

Proposition.  $\mathcal{M}_1(p,q)$ is naturally identified with an “open positroid variety” in $\mathrm{Gr}_p(\mathbf{C}^{p+q})$, divided by its action of $(\mathbf{C}^*)^{p+q}$

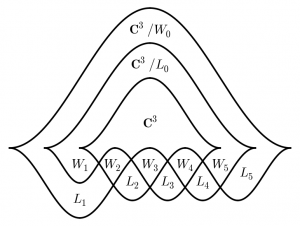
To explain why, exchange a sheaf on  a rainbow front, such as

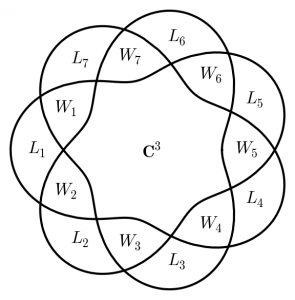
for a “spirograph” front

(Each $L$ is a line in $\mathbf{C}^3$, each $W$ is a plane in $\mathbf{C}^3$.  In the spirograph figure, put $W_7 := W_0$, $L_6 := L_0$, $L_7:=W_1 \cap W_0$, $W_6 := L_0 + L_5$.)  The moduli of constructible sheaves on the rainbow is isomorphic to the moduli of constructible sheaves on the spirograph, STZ Proposition 6.14.

There is probably a direct topological reason for this, a contactomorphism from $T^{\infty}\mathbf{R}^2$ to itself that carries the Legendrian knot over rainbow to the Legendrian knot over the spirograph.

Note in the spirograph figure the $W$s are determined by the $L$s, e.g. $W_i = L_{i-1}+L_i$ by the crossing condition.  (The $L$s are also determined by the $W$s).  In general a point in $\mathcal{M}_1(p,q)$ is determined by $p+q$ lines in $\mathbf{C}^p$.  The lines are subject to the following open condition: considering the indices $1,\ldots,p+q$ in their obvious cyclic order, any set of $p$ consecutive lines must be in general position.  (Thus $L_1,L_2,L_3$ and $L_7,L_1,L_2$ span $\mathbf{C}^3$, but it is allowed that $L_7 = L_3$.)

We can present each line as a nonzero column vector, and a point in $\mathcal{M}_1(p,q)$ as a $p \times (p+q)$-matrix.  We can scale the columns arbitrarily resulting in a right action of $(\mathbf{C}^*)^{p+q}$ or change the basis of $\mathbf{C}^p$ resulting in a left action of $\mathrm{GL}_p(\mathbf{C})$.  The equation

$$\left[\mathrm{GL}_p \backslash \mathrm{Mat}_{p \times (p+q)}\right]/(\mathbf{C}^*)^{p+q}=\mathrm{GL}_p \backslash \left[\mathrm{Mat}_{p \times (p+q)}/(\mathbf{C}^*)^{p+q} \right]$$

(“Gelfand-Macpherson duality”) gives an identification of $\mathcal{M}_1(p,q)$ with a quotient of an open $U \subset \mathrm{Gr}_p(\mathbf{C}^{p+q})$ by $(\mathbf{C}^*)^{p+q}$.

$U$ is the set of those $p$-planes whose $I$th Plucker coordinates are nonvanishing, where $I$ runs through the $p+q$ different $p$-element intervals of the cyclically ordered set $\{1,\ldots,p+q\}$.  This is an example of an open positroid variety, for the most generic positroid.  My conjecture about torus knots is motivated by a famous cluster structure due to Scott on the coordinate ring of $U$, which is of finite type only for $(p,q) = (2,n)$ or $(3,4)$ or $(3,5)$.

 

Compactification.

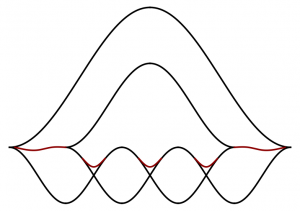
Roughly speaking for a general front $\Phi$, a point of $\mathcal{M}_1(\Phi)$ is a bunch of vector spaces subject to (1) closed conditions (containment) coming from strands and (2) open conditions (transversality) coming from cusps and crossings.  You can compactify $\mathcal{M}_1(\Phi)$ — lots of ways — by relaxing the conditions (2).  A geometric interpretation of these compactifications comes from adding some Legendrian chords to the Legendrian knot, and allowing the chords to appear in singular support (but with multiplicity zero).

Each chord determines a divisor at the boundary of the compactification (in the figure, where the map across the chord becomes zero), which is $\mathcal{M}_1$ of a simpler front diagram (e.g. by smoothing a crossing).

Is the compactification $\mathrm{Gr}_p(\mathbf{C}^{p+q})/(\mathbf{C}^*)^{p+q} \supset \mathcal{M}_1(p,q)$ of this form?  One of the results of Knutson-Lam-Speyer is that positroids give a stratification of $\mathrm{Gr}_p(\mathbf{C}^{p+q})$, perhaps they arise by smoothing the crossings in the spirograph figure.