Here is some information about perverse sheaves on Riemann surfaces. At the end is a point I’m confused about.
A perverse sheaf is a constructible chain complex of sheaves \(P\) that obeys the following conditions: 1. except for finitely many points \(x\), the stalk of \(P\) at \(x\) is concentrated in degree zero, 2. at those points (call them singularities), the stalk is concentrated in degrees zero and minus one, and the costalk is concentrated in degrees zero and plus one. Perverse sheaves make an abelian category in which every object has finite length.
Perverse sheaves are local systems, except near one of the singular points. The building block is the case where \(X\) is the affine line and \(0\) is the unique singular point.
Deligne observed in a 1981 letter to MacPherson that in this case the category of perverse sheaves is equivalent to the category of tuples \(V,W,p:V \to W, q:W \to V\) subject to the condition that \(1 – qp:V \to V\) is invertible. \(V\) is the stalk of \(P\) at \(1\), which can also be identified with the relative cohomology \(H^1(\mathrm{U}(1),\{1\};P)\). \(W\) is the cohomology of the pair \(H^1(X,\{1\};P)\) — note this doesn’t change if we replace \(\{1\}\) with a half-plane, \(W\) is a Morse group. The map \(p:V \to W\) is the connecting homomorphism for the pairs \(X,\{1\}\) and the map \(q:W \to V\) is the restriction homomorphism for the inclusion \(\mathrm{U}(1),\{1\} \to X,\{1\}\). The composite \(qp\) is a differential computing the cohomology of \(\mathrm{U}(1)\) with coefficients in \(P\) — in other words it is one minus the monodromy of \(P\) around \(0\).
Let \(V,m\) be a local system on \(X – \{0\}\) with fiber \(V\) and monodromy \(m\). There are three functorial extensions to a perverse sheaf on \(X\):
1. Take \(W = V\), \(p = 1-m\), \(q = 1\). This is the \(*\)-extension.
2. Take \(W = V\), \(p = 1\), \(q = 1-m\). This is the \(!\)-extension.
3. Take \(W = \mathrm{image}(1-m)\), \(p = 1-m\), \(q =\) inclusion map. This is the IC extension.
When \(m\) is regular unipotent, there is a fourth, less functorial “tilting” extension: take \(W = V\) plus a one-dimensional vector space, let \(p\) be the inclusion map, and let \(q\) send the one-dimensional summand to the invariant line of \(m\).
To be really explicit, the tilting extension of the constant sheaf on \(X – \{0\}\) has \(V = k\), \(W = k^2\), \(p = (1,0)^T\), \(q = (0,1)\). Call this sheaf \(T\).
If \(1 – qp\) is invertible, so is \(1 – pq\), leading to the auto equivalence \((V,W,p,q) \mapsto (W,V,q,p)\). This is the Fourier transform. The Fourier transform of a tilting sheaf is an IC sheaf. In particular the Fourier transform of \(T\) is the IC extension of a rank two local system with unipotent monodromy around \(0\).
Question
There is a claim at the end of Nadler-Zaslow, that the tilting extension of the constant sheaf on \(X – \{0\}\) has a holomorphic Lagrangian representative given by the graph of \(dz/z^2\). Let’s call the cotangent coordinate \(y\), our holomorphic Lagrangian representing \(T\) is \(yz^2 = 1\).
Naively, the Fourier transform should just exchange the role of \(y\) and \(z\), i.e. regarding \(z\) as the cotangent coordinate should give us a perverse sheaf on the \(y\)-line with two-by-two unipotent monodromy around \(0\).
But because the projection from \(yz^2 = 1\) to the \(y\)-line has no critical points, I would expect the local system you build to just be the pushforward, and that’s not unipotent. Is there a critical point hiding at \(0\) or \(\infty\)?
Nadler’s Springer-theory paper has some discussion of the Fourier transform and “balanced branes.” Maybe this puzzle is resolved there.
PS: (November 7) Nothing to do with balanced branes. This is probably best understood as an example of a GMN wall that has both endpoints on a puncture (in particular, that does not touch any critical value).
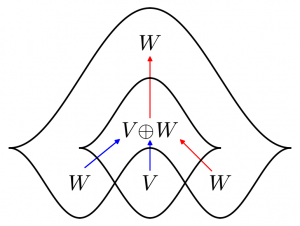
Something else interesting. Representations of $\bullet \leftrightarrows \bullet$, i.e. perverse sheaves on $\mathbf{C}$ locally constant away from $\{0\}$, are the same as constructible sheaves with singular support in the Hopf link, which you can present in the plane. E.g. $(V,W,p:V \to W,q:W \to V)$ becomes
where the red arrows are the inclusion and projection maps, the blue arrows are $(p,1_W)$ and $(1_V,q)$.
Of course there is a critical point at \(\infty\). What would GMN do with this Lagrangian? They would pick two branches of \(y z^2 = 1\), i.e. \(z = \pm 1/\sqrt{y}\), which regarded as one-forms are \(\pm dy/\sqrt{y}\). The difference of these two branches is \(2 dy/\sqrt{y}\). The differential equation
$$
2dy/\sqrt{y} = e^{i \theta} dt
$$
where \(t\) is the parameter of a path and \(\theta\) is the mystery parameter from our email discussions, has solutions \(y(t) = (\frac{1}{4} e^{i \theta} t + C)^2\). If \(C = 0\) (is there some reason it should be?) this looks like a single wall or ray from \(0\) to \(\infty\) at angle \(2\theta\), does crossing change monodromy by something non-semisimple?
By the way, in Boalch’s paper arxiv:1111.6228, the moduli of pairs \((p,q)\) with \(1+pq\) invertible plays some kind of role, which is isomorphic to the above by sending \(p \mapsto p, q \mapsto -q\). Boalch calls them “van den Bergh’s quasi-Hamiltonian spaces \(\mathcal{B}(V,W)\), apparently after arxiv:0410528 and arxiv:0703293. He explicitly mentions (page 12) that these spaces are moduli of D-modules on a disk, but I didn’t dig any further.