HOME

OVERVIEW

APPLICATIONS

  • Geometry
  • Soap Bubbles
  • Medical Imaging
  • Robotics
  • Fluids
  • Semiconductors
  • Wave Propagation
  • Image Denoising
  • Optimal Design
  • Seismic Analysis
  • Tumor Modeling
  • Optimal Control
  • InkJet Plotters
  • Traveling Salesmen
  • ViscoElastic Flow
  • Pinching Droplets
  • Chemical Pathways

    INTERACTIVE APPLETS

    HISTORY OF THE METHODS/FLOW CHART

    PUBLICATIONS

    EDUCATIONAL MATERIAL

    ACKNOWLEDGEMENTS

    ABOUT THE AUTHOR/CV








    Copyright:
    1996-2010
    J.A. Sethian

    • Segmentation in Medical Imaging

    Imagine that you are given an image, say a medical (MRI or CT) scan. Below is a digital subtraction angiogram (DSA):


    Suppose you want to extract the important feature within the image; in this case, the outline of the artery. One idea is to look for places where there is a big jump in intensity between neighboring pixels. However, it is hard to pick a good value for the jump; too small and you get extra boundaries; too large and you miss the whole show. Another problem is that you can get fooled by large spikes of noise.

    An Evolving Interface Approach to Active Contours

    A different approach comes from initializing a small circle inside the region of interest, and allowing it to grow outwards until it reaches the desired boundary.
    We use a Fast Marching Method to propagate the initial seed point outwards, followed by a level set method to fine tune the result. The key idea is to evolve the curve outwards with a speed that depends on the image itself:

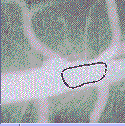
    • When the curve passes over places where the image gradient (that is, the change in value from one pixel to the next) is small, we let the curve expand quickly.
    • When the curve passes over places where the image gradient is large, we suspect we are near the boundary, and slow the curve down.
    • In addition, we include a curvature term to the speed to add a little surface tension to the expanding contour.
    Arterial Tree (1.3 MB) Femurs and Surrounding Soft Tissue (232K)
    Beating Heart(1.3 MB) Reconstruction of Brain(232K)
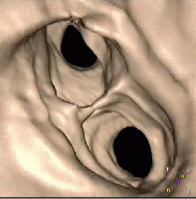
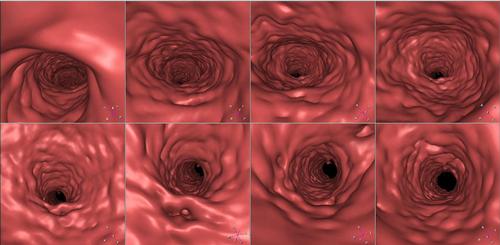
    Aortic Fly through Virtual Endoscopy Trachae Fly through

    Interactive Java Applet

    Try out an interactive Java applet for automatic shape recovery



    Advantages of this Approach

    The level set approach allows the evolving front to change topology, break, and merge, which means that the evolving front can extract the boundaries of particularly intricate contours. In addition, the method works in three dimensions with almost no change, so three dimensional surfaces can be extracted as well.

    Details

    The calculation was performed using a level set method to track the motion of an initial interface, which is embedded as the signed distance function. The resulting level set equation for front propagation is then updated using a first order in time, central difference in space scheme. The approach is similar to that of active contour models, in that a speed function is synthesized from the image gradient, and includes an expansive balloon force, a curvature-driven surface tension term, and Gaussian mollifier based on the local image-gradient. Additional movies

    References

    • A Topology Independent Shape Modeling Scheme , Malladi, R., Sethian, J.A., and Vemuri, B., Proceedings of SPIE Conference on Geometric Methods in Computer Vision II, Vol. 2031, San Diego, California, pp. 246--258, July 1993.
      List of downloadable publications


    • Shape Modeling with Front Propagation: A Level Set Approach , Malladi, R., Sethian, J.A., and Vemuri, B., IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol. 17, No. 2, February 1995.
      List of downloadable publications