HOME

OVERVIEW

APPLICATIONS

  • Geometry
  • Soap Bubbles
  • Medical Imaging
  • Robotics
  • Fluids
  • Semiconductors
  • Wave Propagation
  • Image Denoising
  • Optimal Design
  • Seismic Analysis
  • Tumor Modeling
  • Optimal Control
  • InkJet Plotters
  • Traveling Salesmen
  • ViscoElastic Flow

    INTERACTIVE APPLETS

    HISTORY OF THE METHODS/FLOW CHART

    PUBLICATIONS

    EDUCATIONAL MATERIAL

    ACKNOWLEDGEMENTS

    ABOUT THE AUTHOR/CV








    Copyright:
    1996-2010
    J.A. Sethian

    • Geometry

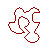
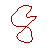
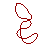
    Imagine a closed curve lying on this page, and don't let the curve cross over itself. (This is known as a simple, closed curve). For example, take a piece of rope, glue the two ends together, and drop it on the ground, making sure that the rope doesn't cross over itself.

    Simple Closed Curve Not Simple Curve Even Less Simple


    The curvature measures how fast a curve bends at any spot. For example, a circle has a constant curvature because it always is turning at the same rate; a smaller circle has a higher constant curvature because it turns faster.

    Now, suppose each piece of the curve moves perpendicular to the curve with speed proportional to the curvature. Since the curvature can be either positive or negative (depending on whether the curve is turning clockwise or counterclockwise), some parts of the curve move outwards while others move inwards. This is called "motion under curvature".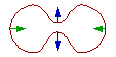

    Blue arrows are where the curvature is negative
    Green arrows are where the curvature is positive

    A Famous Theorem

    A famous theorem in differential geometry, proved less than ten years ago, says that any simple closed curve moving under its curvature collapses nicely to a circle and then disappears. That is, no matter how wildly twisting a curve is, as long as it is simple, it will "relax" to a circle and then disappear.

    Movie of Weird Curve Collapsing under Its Curvature
    (305K)

    Why Care?

    Although the theorem is interesting in its own right, it has wide applications. The surface tension of an interface, like a soap bubble, is proportional to its curvature; for example, the dynamics of ink in an ink jet plotter is affected by its surface tension. Other applications include the evolution of boundaries between fluids and removing noise from an image.


    An Interactive Java Applet:

    Draw a curve and let it evolve under your own speed law

    Details

    The movie was made using a level set method to track the motion of an interface evolving according to its curvature. The curve is embedded as the zero level set of the signed distance function. The level set equation is updated using a first order in time, central difference in space approximation. Periodic boundary conditions are taken on a 200x200 grid.

    References

    Sethian, J.A., A Review of Recent Numerical Algorithms for Hypersurfaces Moving with Curvature-Dependent Speed, Journal Differential Geometry, 31, pp. 131-161, 1989.
    This paper List of downloadable publications