Exercise:Prove that ![]() is irrational.
is irrational.
Definition:We define an object called ![]() by
by
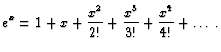
This is an example of an object called a power series. ``Power'' because
it is made of powers of ![]() and ``series'' for obvious reasons. For
us, a power series is not much different from a polynomial - we just
have infinetely many terms (pieces) at the same time. We still can
multiply and add power series according to the same rules.
and ``series'' for obvious reasons. For
us, a power series is not much different from a polynomial - we just
have infinetely many terms (pieces) at the same time. We still can
multiply and add power series according to the same rules.
Exercise:Check that
![]() , so we can write
, so we can write
Exercise:Prove that ![]() .
.
Consider now the ring of polynomials in two variables ![]() and
and
![]() . These are objects of the type
. These are objects of the type
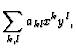
Exercise:Work out the addition, the multiplication, the
differentiations with repect to ![]() and
and ![]() .
.
The main property of the exponential function is
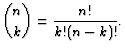
Exercise:Work out the details.
![]()
Our next goal is to compute ![]() . Namely, if
. Namely, if ![]() is a polynomial,
what would be
is a polynomial,
what would be ![]() ?
?
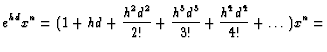 | |||
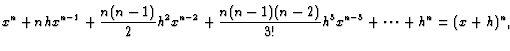 |
|||
Remark:In calculus, the formula
![]() is called the Taylor
expansion formula. It is an important formula, and it includes many
others as special cases. For example, if
is called the Taylor
expansion formula. It is an important formula, and it includes many
others as special cases. For example, if ![]() is a polynomial then
as we saw this is just the Newton binomial formula.
is a polynomial then
as we saw this is just the Newton binomial formula.
If
![]() then the Taylor expansion formula (where
then the Taylor expansion formula (where ![]() is set
to zero) becomes
is set
to zero) becomes ![]() 4
4![]() (with
(with ![]() replaced by
replaced by ![]() ) - just
the formula for the geometric progression.
) - just
the formula for the geometric progression.
Note that in calculus, the Taylor expansion formula does not necessarily
hold for all values of ![]() . But in algebraic formal sense it always true.
. But in algebraic formal sense it always true.
Exercise:a) For what values of ![]() is the formula
is the formula ![]() 4
4![]() true?
true?
b) Let ![]() for
for
![]() and
and
![]() for
for ![]() . Use
calculus to show that
. Use
calculus to show that
![]() for all
for all ![]() .
.
Now let us consider two operation: ![]() and
and ![]() .
.
Exercise:Let ![]() and
and ![]() are two letters such that
are two letters such that ![]() . Prove that
. Prove that
![]() by multiplying the corresponding series and moving
all
by multiplying the corresponding series and moving
all ![]() 's to the right and all
's to the right and all ![]() 's to the left.
's to the left.
Remark:Our notations are not completely random - ![]() is the standard notation
for the Plank constant, and
is the standard notation
for the Plank constant, and ![]() is traditionally related to the word
quantum.
is traditionally related to the word
quantum.