Physical Effects/Overview of Mechanism:
Level Set Methodology:
Results and Sample Simulations:
In the below examples, we assume luminiscent re-emission; thus, re-emitted and redeposited particles are ejected with uniform angle probability.
-
Effect of Re-deposition on Uni-directional Etching: Various Sticking Coefficients
Under directional etching directly from the vertical, the two figures contrast complete etching (sticking coefficient 1.0) with etching plus deposition, in which the total amount of mass removed is again re-deposited.
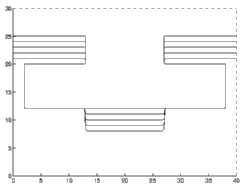
|
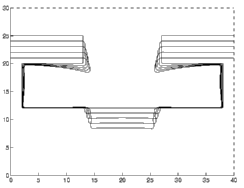
|
| Full Etching | Etching plus Re-deposition |
-
Effect of Sticking Coefficient on Deposition:
Next, we vary the sticking coefficient for a pure deposition process. A uni-directional deposition beam enters from the vertical, and the sticking coefficient varies from 1.0 down to .2.
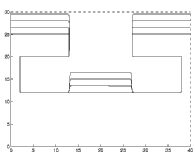
|
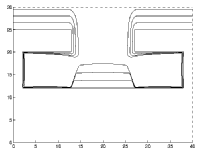
|
| Full Deposition: Sticking Coefficient 1.0 | Full Deposition: Sticking Coefficient .5 |
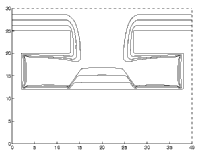
|
Full Deposition: Sticking Coefficient .2 |
-
Three-Dimensional Simulations: Deposition into Via
Finally, we vary the sticking coefficient for a pure deposition process in 3D. The example is fully three-dimensional; no two-dimensional simplications are used whatsoever. A full source deposition beam comes from a plate above, and the sticking coefficient varies from 1.0 down to .001.

|

|
| Full Deposition: Sticking Coefficient 1.0 | Full Deposition: Sticking Coefficient .1 |

|
Full Deposition: Sticking Coefficient .001 |