Directional Deposition and Etching: Ion-Milling and Non-convex Sputter Laws

Physical Effects/Overview of Mechanism:

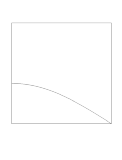
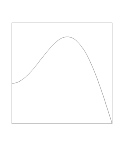
We now analyze a deposition/etching effect, including the effects of visibility. Let Y(theta) be the yield function, that is the effectiveness of the etching/deposition process as a function of the angle theta between the normal to the surface and the direction of the beam. In the case of pure isotropic deposition, F(theta)=1 [in the case of etching, F(theta)=-1]. In the case of simple dependence on incoming angle, we would have that F(theta) = cos theta, thus, no ion-milling takes place if the beam is tangential to the surface, while the full effect takes place if the beam is normal to the surface.
As is well-known, there are other cases in which the ion-milling term is most effective at an angle other than theta=0; that is, the yield is largest at some intermediate angle located between normal to the surface and tangential to the surface. These three typical yield curves as shown in the figures below.
Isotropic Yield Curve Cosine Yield Curve Ion-Milling Yield Curve

As is well-known, the last case produces faceting related to the optimal angle. The difficulty in traditional numerical methods lies in determining how to advance the surface at places where the normal is not defined.

Level Set Methodology:

The level set methodology advances the surface by solving the appropriate initial value partial differential equation, using the correct viscous limit of the Hamilton-Jacobi equation. Thus, the normal is correctly defined as the weak limit in places where differentiability is lost. In the case of strong ion-milling effects, the resulting equation becomes non-convex; while non-convex update schemes are then required, this does not pose any particular difficulty.

Results and Sample Simulations:



We consider three different speed functions:
Initial Saddle Shape Intermediate Shape
Final Saddle Shape Final Shape Rotated


Return to Overview Page