


Next: A two-compartment model of
Up: yakovlev
Previous: Introduction
One of the few near-universal observations about
solid tumors is that almost all decelerate, i.e.
reduce their specific growth rate 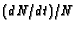 , as they grow
larger [1, 2].
Consequently Eq. 1 is often generalized
to a non-linear first order ODE which incorporates growth
deceleration [1, 3 -
6]:
, as they grow
larger [1, 2].
Consequently Eq. 1 is often generalized
to a non-linear first order ODE which incorporates growth
deceleration [1, 3 -
6]:
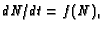 |
(2) |
where 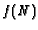 is an appropriate function.
Observed tumor growth is consistent with the assumption that the
tumor would reach some given limiting cell number,
the host carrying capacity
is an appropriate function.
Observed tumor growth is consistent with the assumption that the
tumor would reach some given limiting cell number,
the host carrying capacity 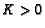 , if treatment or death did
not intervene.
The most commonly used example of an ODE which incorporates this
assumption is the generalized logistic
equation. This equation is of the replicator type
[7] and has one global attractor for
the region
, if treatment or death did
not intervene.
The most commonly used example of an ODE which incorporates this
assumption is the generalized logistic
equation. This equation is of the replicator type
[7] and has one global attractor for
the region 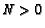 , at a point
, at a point 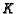 , as follows:
, as follows:
![$\displaystyle f(N) = N F(N/K) = ( \mu N / \nu ) \biggl [ 1 - (N/K)^{\nu} \biggr ] , \quad \quad \mu > 0 .$](img18.gif) |
(3) |
Here 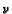 is real and the value
is real and the value 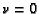 is to be understood as a
limit; taking the limit gives the Gompertz equation [8,
9]:
is to be understood as a
limit; taking the limit gives the Gompertz equation [8,
9]:
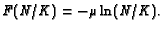 |
(4) |
Eq. 1 can be obtained from Eqs. 2 and
3 by
restricting attention to the region 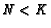 and then taking the
limit
and then taking the
limit
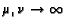 with
with 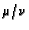 fixed at
fixed at
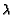 . One other special case is
. One other special case is 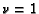 , the logistic
equation which Eq. 3 generalizes.
Roughly speaking,
, the logistic
equation which Eq. 3 generalizes.
Roughly speaking, 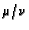 in Eq. 3
replaces
in Eq. 3
replaces 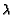 and
and 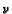 governs how fast the
tumor approaches the limiting number
governs how fast the
tumor approaches the limiting number 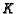 [6].
[6].
One-ODE models have frequently been applied
to experimental and clinical tumors, and to tissue culture
models (surveys in
[1, 5]). The most systematic
clinical application of Eq. 3, to breast tumors,
suggested an optimal
value of close to 0.25 for 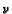 [6].
[6].
In analyzing tumor treatments or experiments on cell killing by
external agents, a very common assumption
(often made implicitly) is that treatment modifies Eq.
2 by adding an extra term, as follows:
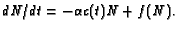 |
(5) |
Here 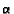 is a positive constant, the strength
of the chemotherapeutic agent, and
is a positive constant, the strength
of the chemotherapeutic agent, and
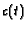 is the agent
concentration at the location of the tumor, governed
by treatment schedule and pharmacodynamic effects.
The direct proportionality of the killing term
to
is the agent
concentration at the location of the tumor, governed
by treatment schedule and pharmacodynamic effects.
The direct proportionality of the killing term
to 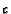 and to
and to 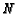 corresponds to
mass-action chemical
kinetics for the reaction of a therapeutic agent and a cell.
corresponds to
mass-action chemical
kinetics for the reaction of a therapeutic agent and a cell.



Next: A two-compartment model of
Up: yakovlev
Previous: Introduction
Rainer &
1999-10-20
![]() [6].
[6].