|
PEXSI
|
The Pole EXpansion and Selected Inversion method (PEXSI) is a fast method for evaluating certain selected elements of a matrix function. PEXSI is highly scalable on distributed memory parallel machines.
Given a sparse square matrix \(A\) and a certain function \(f(\cdot)\), the basic idea of PEXSI is to expand \(f(A)\) using a small number of rational functions (pole expansion)
\[ f(A) \approx \sum_{l=1}^{P} \omega_l(A-z_l I)^{-1}, \]
and to efficiently evaluate \(f(A)_{i,j}\) by evaluating selected elements \((A-z_l I)^{-1}_{i,j}\) (selected inversion).
The currently supported form of \(f(\cdot)\) include:
\(f(z)=\frac{2}{1+e^{\beta (z-\mu)}}\): Fermi-Dirac function. This can be used as a "smeared" matrix sign function at \(z=\mu\), without assuming a spectral gap near \(z=\mu\). This can be used for evaluating the electron density for electronic structure calculation. See pagePEXSISolve for an example using PEXSI for electronic structure calculation.
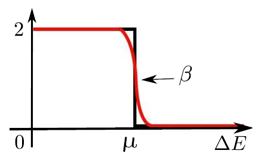
For sparse matrices, the PEXSI method can be more efficient than the widely used diagonalization method for evaluating matrix functions, especially when a relatively large number of eigenpairs are needed to be computed in the diagonalization method. PEXSI can also be used to compute the matrix functions associated with generalized eigenvalue problems, i.e.
\[ f(A,B):= V f(\Lambda) V^{-1} \approx \sum_{l=1}^{P} \omega_l(A-z_l B)^{-1}, \]
where \(V,\Lambda\) are defined through the generalized eigenvalue problem
\[ A V = B V \Lambda. \]
PEXSI is most advantageous when a large number of processors are available, due to the two-level parallelism. For accurate evaluation, the pole expansion usually takes around \(P\approx 80\) poles. All the \(80\) matrices can be inverted independently among different groups of processors. The parallel selected inversion method (PSelInv, which is included in PEXSI) can scale well to \(256\sim 1024\) or more processors depending on the sparsity of the problem, and the system size. Therefore it is most advantageous to use PEXSI when more than 1000 processors are available. For some problems we have also observed that it can be advantageous to use PEXSI using hundreds to thousands of processors.
The diagonalization method evaluates a matrix function \(f(A)\) by
\[ f(A) = V f(\Lambda) V^{-1}, \]
where the orthonormal matrix \(V=[v_1,\ldots,v_N]\), and the diagonal matrix \(\Lambda=\mathrm{diag}(\lambda_1,\ldots,\lambda_N)\) are defined through the eigenvalue problem
\[ A V = V \Lambda. \]
It is often the case that not all eigenvalues \(\{\lambda_i\}\) are needed to be computed, depending on the value of \(f(\lambda_i)\).
For structurally symmetric matrices (i.e. \(A_{i,j}\ne 0\) implies \(A_{j,i}\ne 0\)), we define the selected elements of a matrix \(B\) with respect to a matrix \(A\) as the set \(\{B_{i,j}\vert A_{i,j}\ne 0\}\).
A commonly used case in PEXSI is the selected elements of \(A^{-1}\), which corresponds to the set \(\{A^{-1}_{i,j}\vert A_{i,j}\ne 0\}\).
 1.8.5
1.8.5