Research
My current research interests are in numerical PDE and
adaptive mesh refinement
Projects
Eulerian Elastic Surfaces
| In my thesis work, I am devloping a set of
numerical methods for simulating elastic surfaces in an eulerian,
finite difference setting. These methods, an extension of traditional
level set methods, are designed to work efficiently and accurately in
fluid-structure interaction frameworks that use eulerian grids to solve
the fluid equations.
|
BoxLib-RAMR
| BoxLib
is a block-structured Adaptive Mesh Refinement framework for large scale
scientific simulations. Working in LBL's CCSE I co-developed a new
model for the structure of AMR simulations called Region-based AMR.
This model allows greater freedom in decomposing block-structured AMR
domains which permits greater computational efficiency for a number of
problems as well as opening a host of options for tackling exascale problems
Early implementations in the BoxLib-based NYX code have been successful and
the initial publication is forthcoming.
|

|
Pykaryote
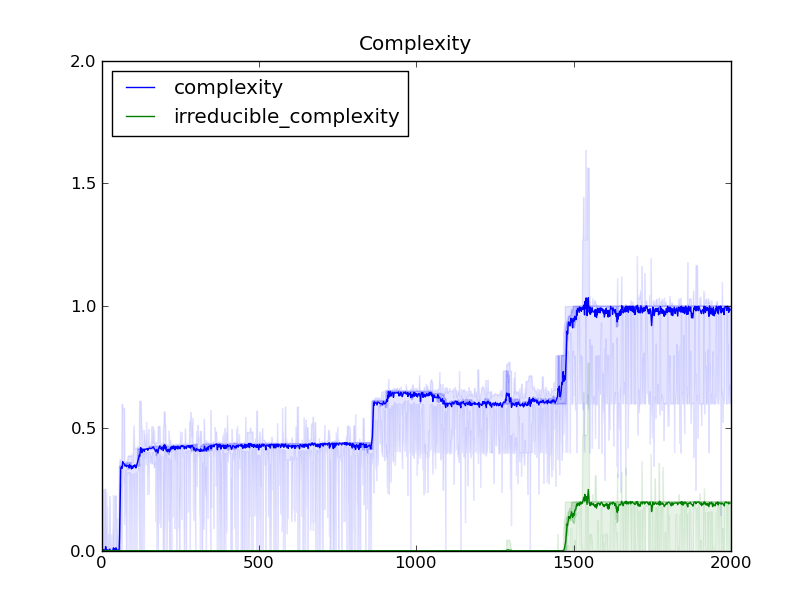
| Pykaryote is a python/cython agent-based model for studying
the evolution of irreducible biological complexity. It is
currently being developed in collaboration with a group from
Calvin College. More information will be available following
the publication of our initial paper. |
|
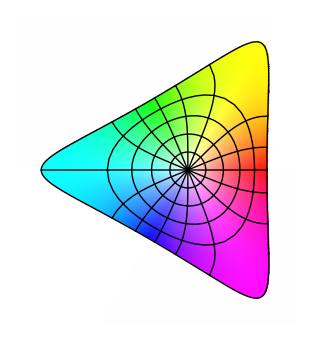
Riemann Mapping in Sage
| I developed and continue to maintain the package that the
Sage mathematics software system
uses to perform general numerical Riemann Mapping. |
|
Papers and Presentations
- Almgren, A. Bell, J. Lijewski, M. Lukić, Z. Van Andel, E.
"Nyx: A Massively Parallel AMR Code for Computational Cosmology".
ApJ, 765, 39, 2013.
- Bolt, M. Snoeyink, S. Van Andel, E. “Visual representation
of the Riemann map and Ahlfors map via the Kerzman-Stein equation”.
Involve 3-4: 405-420, 2010.
- Van Andel, E. “Region-Based AMR: A New AMR Paradigm in BoxLib.
SIAM-CSE13 FastMath Minisymposium, Boston, MA. Feb 2013.
- Van Andel, E. “Riemann Mapping in Sage”. Michigan
Section of the MAA Annual Meeting, Kalamazoo, MI. May 2011.
- Van Andel E. Haarsma, L. “Modeling the Evolution of
Irreducible Complexity” (Possible Title).In preparation.


