UC Berkeley Summer 2017

Home | Contact Info | FAQ | Research Groups | Apply | Poster
(source)
Group 1: Curvature Shortening Flow
Project Leader: Patrick Wilson
A geometric flow is a way of deforming a geometric object from one shape into another, possibly nicer, shape. More precisely, a geometric flow is a partial differential equation that describes how a geometric object deforms or evolves in time. The most famous example of such a flow is the Ricci flow, used in Perelman's proof of the Poincare Conjecture.
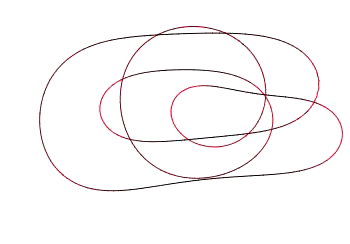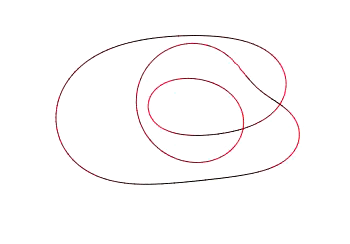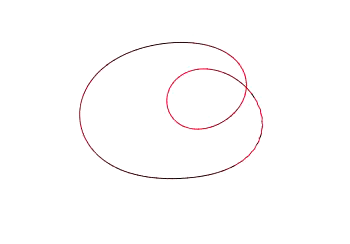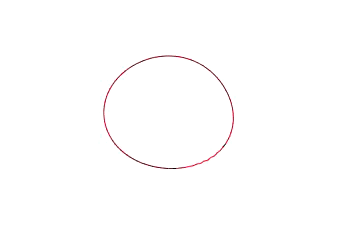
This research program will focus on the curvature shortening flow (CSF), which describes how a curve evolves in the plane. Grayson's Theorem states that under the CSF, any embedding of a circle in the plane will shrink to a point in finite time, while becoming more circular. After understanding this result, we will look at extensions such as computer algorithms for solving this PDE, thereby giving visual examples of the flow, and evolutions of networks.
Prerequisites: Students should be familiar with undergraduate real analysis. Some background in differential geometry and/or partial differential equations would be helpful. In addition, some programming knowledge may be useful.
Background reading : Differential geometry of curves, as in Chapters 1-3 of "Elementary Differential Geometry" by Andrew Pressley
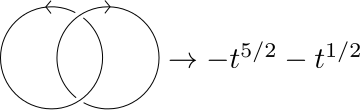
Group 2: Quantum Invariants of Three-Dimensional Manifolds
Project Leader: Kevin Donoghue
Many topological invariants involve a combinatorial construction (like the Euler characteristic of a graph), or a geometric construction (like the zeroes of a generic vector field). In 1989 Ed Witten predicted the existence of an invariant of three-dimensional manifolds that turned out to have a representation-theoretic construction. For example, the three-dimensional sphere is assigned a number that comes from the theory of infinite-dimensional Lie algebras.
Witten's invariant and its spinoffs are now loosely grouped under the term "quantum invariants." Even the simplest cases are already interesting--the invariants fit into a structure called a "topological quantum field theory", or "TQFT." We will deal with the "T" part and can safely ignore the "QFT" part.
Importantly, the TQFT package includes not only the invariant of the three-dimensional manifold, but also surface invariants, representations of mapping class groups, interesting algebras and categories, and link invariants. In this program you will compute these things in simple cases, for example in the “finite group” model of Dijkgraaf and Witten. Because the computations can get quite involved, it is easy to glean from the computations an understanding of how TQFTs work in general. In particular, although Witten's original invariant is still somewhat mysterious, the simplest quantum invariants give a lot of intuition for what makes the original one tick.
You'll need a course in point-set topology, a course in abstract algebra, and a willingness to learn a whole lot of interesting stuff about manifolds, links, and representation theory. Do you need to know all the fancy words in the previous two paragraphs? No, definitely not! There will be lectures to help bring you up to speed.