Math Explorer's Club.

Module on Puzzles -  Antonio Montalbán and Yannet Interian.
(January 13, 20,  February 3, 10, 17 and March 3.)
Ithaca High School.

 
    In this module I'll be giving you many math puzzles of various kinds. Some of them are easier than others. Some are very hard. The idea is to try to solve the puzzles and discuss the solution, or the possible solutions, with other students. The first day we'll do different kind of puzzles. In the following days I'll choose a topic and discuss puzzles related to that topic.

Possible topics are:

Liars and Truth-tellers puzzles.

The setting for these problems is the following. There is this island in the middle of the ocean where there are two kinds of people: the liars and the truth-tellers. The liars always lie. Any question you ask them will be answered with a lie. The truth-tellers always answer the truth.
   Here are a few examples.
  1. You're walking in this island and you meet a native, who could be either a liar or a truth-teller, and you want to know which kind of person he is. So you ask him
       - are you a truth-teller? 
    When he is answering, the volcano makes a loud noise and you cannot hear the answer. So you ask him again
       - Excuse me, I couldn't hear what you said, did you say you were a truth-teller? - and he answers
       - no, I didn't say that, I said I was a liar.
    Is the native a liar or a truth-teller?
      (Hint: Think about what the native's could have answered to the first question, first assuming he's a truth-teller and then assuming he's a liar.)
     
  2. Suppose now that you visit a second island close by. In this second island the people is even more weird. They lie on Tuesdays, Thursdays and Saturdays and they tell the truth the other days. After spending so many days in these islands you forgot which day it is. So you ask one of the islanders:
         - Excuse me sir, what day is today?
         - Saturday - he answers.
         - And, what day is it going to be tomorrow?
         - Wednesday.
    Can you deduce what day is today?

  3.   Now suppose you meet three people, A, B and C form the first island (so they are either liars or truth-tellers). You ask A:
         - How many truth-tellers are among you guys?
    Again, the volcano makes a loud noise when A answers and you can't hear the answer. So you ask B:
         - What did A say? -  and B answers
         - A said that one of  us is a truth-teller and two of us are liars - and then C adds
         - Don't believe what B said, he's lying.
    What class of people are B and C?
There are more liars and truth-tellers puzzles here.
Knots and graphs.
  I'll add more stuff here later.
  1. Draw three houses in a horizontal row. Draw three utilities suppliers beneath them: Gas, Water, Electricity. You should now have six points or boxes on your sheet of paper. The challenge is to connect each house to each utility supplier without any of the nine connection lines crossing. Is it possible? (This problem is very hard!)
Arithmetic and geometry.
  Here are a few examples (I'll add more later):
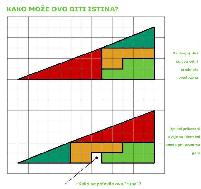  1. what's wrong here?    What's wrong with this picture? (Click to enlarge and translate.)

  2. Bike tracks  In what direction is the bike going? (click to enlarge)

  3. I have three clocks. One is a watch that I wear every day. Then I have an alarm clock that goes back to 12:00am (midnight) when there is a blackout, and I have an electric clock in the kitchen which is not digital. The latter clock stops working if there is a blackout and continues working when the electricity comes back.
       One day I went to sleep after midnight and when I woke up the following morning , the three watches were working but they all had different times: 7:45am, 8:15am and 9:30am. Probably it was because there was a blackout during the night. Assuming that this is what happened, at what time did the blackout started and when did it end?

  4. What is the last digit of the product of the numbers 1, 3, 5, 7, 9, 11,...., 2001, 2003 and 2005?
Rubik's Cube.     2 x 2 x 2 Rubk's cube.

Solving the 3 x 3 x 3 Rubik's cube is very very hard. The smaller 2 x 2 x 2 is not easy either. I really don't expect anybody to come up with a solution. I just expect you'll understand the method I'll show you, which is not simple at all.
   Note that to solve the 2 x 2 x 2 cube is equivalent to solve the corners of the bigger cube. So by learning this method, you're learning the beginning of the method to solve the  3 x 3 x 3 cube.
   We'll learn how to solve the 2x2x2 cube!!!  Here is a sketch of the solution.