February 3.
Math Explorer's Club.
Module on Puzzles
Antonio Montalbán and Yannet Interian.
Ithaca High School.
Sketch
of the Solution.
Here is a quick
sketch of the algorithm that solves the 2x2x2 Rubik's cube, also known
as the Pocket Rubik's cube. A lot of thinking is still
necessary to understand the algorithm and how to apply it. For
more information on the terminology that I use for cube moves and for a
slightly different and more detailed explanation of the solution, go to
Helmsoft.
There are three main steps:
Top Face
I am not going to tell you how to do the top face. You will have to figure it out by yourself, which is not that easy, but it is not impossible either. It might take some time the first time. One hint is the following. If you want to put a corner somewhere, but you don't want to mess up what you have done so far, hide what you have done some far, move the piece you want to move, and then put what you have hidden back to its place.
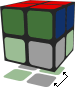
Attention: Remember that the pieces have three sides each. So it is not enough to make just the top face correct, the sides have to match too. The cube should look like in the picture below, where the white pieces are the ones that haven't been accommodated yet.

Place bottom corners.
Now you need to place the bottom corners in the right positions. Don't worry about the orientation of the corners yet, only about the position. We will deal with the orientation in the next step. The way we do this is by applying the following algorithm that swaps two bottom corners. You have to do it enough times to place all the corner in the right positions. The first thing you need to figure out is which two corners you want to swap. Here is the algorithm.
Orient bottom corners
Now that we have positioned the bottom corners, all we need to do is to put each corner in the right orientation. The bad news is that there is no algorithm that rotates one corner. But there is a relatively simple algorithm that rotates three corners. You will have to figure out how to use this algorithm repeatedly until you get all the corners right. Here is the algorithm.
After you have this under control, we could start talking about solving the 3x3x3 cube.
Antonio Montalbán.
Department of Mathematics.
Cornell University.
Ithaca, NY 14853.
There are three main steps:
- Do Top face.
- Put the bottom corners in the right position.
- Fix the orientation of the bottom corners.
Top Face
I am not going to tell you how to do the top face. You will have to figure it out by yourself, which is not that easy, but it is not impossible either. It might take some time the first time. One hint is the following. If you want to put a corner somewhere, but you don't want to mess up what you have done so far, hide what you have done some far, move the piece you want to move, and then put what you have hidden back to its place.
Attention: Remember that the pieces have three sides each. So it is not enough to make just the top face correct, the sides have to match too. The cube should look like in the picture below, where the white pieces are the ones that haven't been accommodated yet.

Place bottom corners.
Now you need to place the bottom corners in the right positions. Don't worry about the orientation of the corners yet, only about the position. We will deal with the orientation in the next step. The way we do this is by applying the following algorithm that swaps two bottom corners. You have to do it enough times to place all the corner in the right positions. The first thing you need to figure out is which two corners you want to swap. Here is the algorithm.
 |
|---|
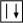  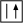  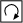   |
Orient bottom corners
Now that we have positioned the bottom corners, all we need to do is to put each corner in the right orientation. The bad news is that there is no algorithm that rotates one corner. But there is a relatively simple algorithm that rotates three corners. You will have to figure out how to use this algorithm repeatedly until you get all the corners right. Here is the algorithm.
 |
|
|---|---|
          |
After you have this under control, we could start talking about solving the 3x3x3 cube.
Antonio Montalbán.
Department of Mathematics.
Cornell University.
Ithaca, NY 14853.
e-mail: antonio at
math.cornell.edu
Updates of this
page can be found at www.math.cornell.edu/~antonio/MEC/mec.html
30/1/2005.
30/1/2005.