Definition.  Fix a prime $p$.  Let $M$ be a manifold.  An $F$-field on $M$ is a locally constant sheaf of perfect rings of characteristic $p$.

Each element of $H^1(M,\mathbf{Z})$ determines an isomorphism class of $F$-fields.  The $F$-field $\mathfrak{f}$ corresponding to the cocycle $z$ has one fiber that is $\overline{\mathbf{F}_p}$, and each loop in $M$ acts on that fiber by taking $p^n$th powers, where $n$ is the degree of $z$ over the loop.  One could replace $\overline{\mathbf{F}_p}$ by any other perfect ring.

The name is stupid.  It reflects my probably misguided hope that these things are similar to $B$-fields.

If $M$ is a symplectic manifold carrying an $F$-field $\mathfrak{f}$, it is interesting to consider Lagrangian submanifolds decorated with locally constant sheaves of modules over $\mathfrak{f}\vert_L$.  If $M = T^* X$, then $\mathfrak{f}$ descends to an $F$-field on $X$, let’s keep on denoting it by $\mathfrak{f}$, and it is interesting to consider constructible sheaves of modules over $\mathfrak{f}$ on $X$.

Example.  If $\mathfrak{f}$ is a nontrivial $F$-field on a circle, whose fiber is an algebraic closure of $\mathbf{F}_p$, its global sections are a finite field $\mathbf{F}_q$.  (While the global cohomology of $\mathfrak{f}$ vanishes in nonzero degrees.)  The category of locally constant sheaves of modules over $\mathfrak{f}$ is equivalent to the category of $\mathbf{F}_q$-vector spaces, again by taking global sections.

One can also put it this way: the data of a locally constant sheaf $\mathcal{L}$ of $\mathfrak{f}$-modules is equivalent to the data of a fiber $\mathcal{L}_x =: V$, together with a $\mathfrak{f}_x$-semilinear (Frobenius-linear) monodromy map $V \to V$, i.e. it gives an $\mathbf{F}_q$-rational structure on the fiber.

Example.  The usual rational structure on the character variety of $\Sigma$ over $\overline{\mathbf{F}_p}$ can be twisted by a mapping class $\phi$.  The $\mathbf{F}_q$-points of this rational structure correspond to locally constant sheaves of $\mathfrak{f}$-modules over the mapping torus of $\phi$,  where $\mathfrak{f}$ is pulled back from the $F$-field on the circle given in the previous example.

Example.  Let $\mathfrak{f}$ be a nontrivial $F$-field on an annulus, and on its cotangent bundle.  Let $\Phi$ be the front projection of the closure of a positive braid, say $b$, and let $\Lambda$ be its Legendrian lift.  Then $\mathcal{M}_1(\Lambda,\mathfrak{f})$ is the set of closed points of a generalized Deligne-Lusztig variety $\mathit{DL}(b)$ defined over $\mathfrak{f}_x$.  Here $\mathfrak{f}_x$ is the fiber of the $F$-field above a point in the top region of $\Phi$.

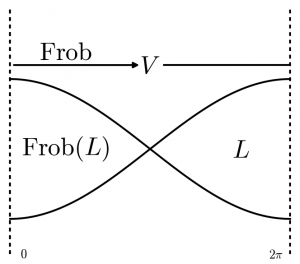
For instance, if $\Phi$ is the closure of a single crossing, then $\mathcal{M}_1(\Lambda,\mathfrak{f}) \cong [(\mathbf{P}^1(\mathfrak{f}_x) – \mathbf{P}^1(\mathbf{F}_q))/\mathrm{GL}_2(\mathbf{F}_q)]$, i.e. a line in $V:= \mathfrak{f}_x^2$ that is not equal to its Frobenius-conjugate.

Each Deligne-Lusztig variety is equipped with a Galois covering whose Deck group is the $\mathbf{F}_q$-points of a nonsplit torus.  (In case of a single crossing as above, the total space is an affine curve of genus $\binom{q}{2}$).  That cover is pulled back from the universal torsor along a map $\mathit{DL}(b) \to BT(\mathbf{F}_q)$.  That has an interpretation here: it’s the microlocal monodromy map $\mathcal{M}_1(\Lambda,\mathfrak{f}) \to \mathit{Loc}_1(\Lambda,\mathfrak{f}\vert_{\Lambda})$.