OVERVIEW
APPLICATIONS
INTERACTIVE APPLETS
HISTORY OF THE METHODS/FLOW CHART
PUBLICATIONS
EDUCATIONAL MATERIAL
ACKNOWLEDGEMENTS
ABOUT THE AUTHOR/CV
Copyright:
1996, 1999, 2006
J.A. Sethian
Stationary Formulation: The Boundary Value PDE View
You are currently in the
topic outlined in red.
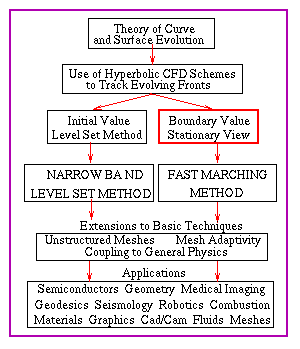
Click on navigable flow chart to go to new topic
click on any text
to go to a new topic.
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
click on any text to go to a new topic. |
can be given. There are several numerical techniques to solve this equation. However, using the previous work on the theory of curve and surface evolution, viscosity theory, upwind schemes, and sorting/causality relationships borrowed from computer science, a particular fast optimal technique, known as the Fast Marching Method can be developed.
New Book and Resource on Level Set and Fast Marching Methods
References for the Eikonal Equation:
-
Partial Differential Equations
:
Garabedian, P., Partial Differential Equations,
Wiley, New York, 1964.
Download publications