SCATTERING RESONANCES AS VISCOSITY LIMITS: A NUMERICAL EXAMPLE

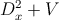
We present a simple numerical companion to Scattering resonances as viscosity limits.

The code viscap.m computes resonances of

D2x + V

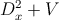
where V is a step potential and the eigenvalues of

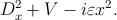
2 2 D x + V - iεx .

The input is given ε,V,r where

V = [V (1),V(2),...V (N )]

are values of the potential in r(K) < x < r(K + 1) where

r = [r(1),r(2),...,r(N + 1)].

In the output [z,w,v] , z is the vector of approximate eigenvalues of Dx2 + V - iεx2 and w is the vector of resonances. Both z and w are pruned to include only the eigenvalues near 0 and to exclude spurious einvalues with arg z near -π∕4. The last output consists of all the computed eigenvalues of the discretization of Dx2 + V -iεx2: most of them are spurious or due to pseudospectral effects.

The resonances are computed using squarepot.m written by David Bindel.

Here are some examples:

viscap(0.5, [ 50 30 50 -30], [ -2 -1 0 1 2]); outputs the figure

[ z, w, v ] = viscap(0.2, [ 40 20 80 ], [-2 -1 1 2]); outputs z,w,v and the figure

The majority of the eigenvalues of the discretization of Dx2 + V - iεx2 are either near arg z = -π∕4 or are due to pseudospectral effects.

plot(v,’r*’,’MarkerSize’,10) outputs the figure

The smaller the ε the more pronounced are the pseudospectral effects: most of the computed eigenvalues are not close to the eigenvalues of the operator.