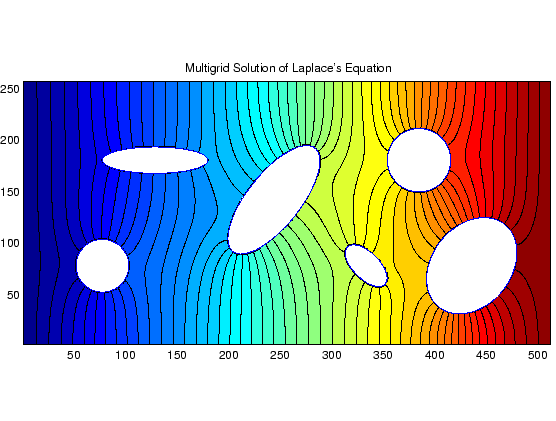


I discretize the problem on a uniform rectangular grid
chosen to be fine enough that the holes are well resolved. I then
use finite differences to set up a linear system of equations
for my multigrid algorithm to solve. For points at the boundaries,
I developed a procedure for generating appropriate stencils to
guarantee that the solution to the linear system agrees to
O(h2) with the solution to the PDE at grid points --
provided that f, sigma, and the boundaries are smooth enough. This
rectangular mesh plays the role of the fine grid in the multigrid
hierarchy. The coarser grids are chosen as shown:
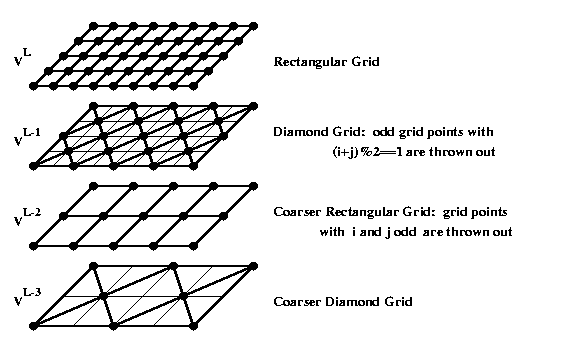
Grid points at all levels which lie in the interior of the holes serve only as place holders in the arrays, and are otherwise unused. The interpolation and restriction operators Tl and Rl are chosen to maximize the degree to which the smoother can interact with the next coarser grid to kill all frequencies of the error while keeping the stencils on each grid level as compact as possible. For geometrical reasons, we take R and T to be transposes of each other with respect to the L2 inner product, and we define the operators Al to make the diagrams commutative:

This choice allows us to interpret the coarse grid problem at level l as the restriction of the fine grid problem to the subspace Image(Tfine ...Tl+1) of the fine grid. I have found Gauss-Seidel to work best as the smoother. My method for choosing the interpolation operators keeps the stencils 3 by 3 away from the boundaries, and allows them to grow as large as 7 by 7 near the boundaries. Here we see the solution on the coarsest rectangular grid levels:

Note that even though some of the holes have been completely lost on the coarsest levels, these levels are still serving their purpose, which is to damp components of the error which the smoother at the next level up does not deal with effectively. Only on the fine grid do we care that the system of equations is accurately modeling the PDE. The sole purpose of the coarse grids is to provide a mechanism for getting the answer on the fine grid fast. The geometrical interpretation mentioned above means that the top few grid levels may safely be thought of as discretizations of the PDE, but the coarsest levels should not be thought of that way.
I ran my parallel multigrid code on a 140 processor Alpha Beowolf cluster called Avalon at Los Alamos National Laboratory. The machine runs Linux with the freely available message passing library MPICH. I found that the convergence rate was completely independent of problem size, requiring remarkably few iterations to reach machine precision. With just six F-cycles with no smoothing on the way down and two sweeps of Gauss-Seidel at each level on the way up, I get residuals with max norms around 10-15 for problems with the number of variables ranging from 128x256 to 1024x2048. On a single processor Intel Pentium III running at 500 MHz, I solved the 256 by 512 problem shown at the top of this web page in 13 seconds. Using 16 processors on Avalon, I solved the 1024 by 2048 problem in 59 seconds. Thus with 16 commercial processors connected together with relatively inexpensive fast ethernet ports and running free software it was possible to solve a 2,100,225 by 2,100,225 system of linear equations which was neither block-Toeplitz tridiagonal, symmetric, nor tightly banded, to machine precision in under a minute.