q-exponent and q-differentiation

Many objects have their quantum versions. We describe here the q-versions of the exponential function and the differentiation.

Recall that the usual derivative $ d$ is a linear map such that $ dx^k=kx^{k-1}$. As before, linear means that we differentiate term by term, see $ ($2$ )$ above.


Definition:Define q-derivative $ D_q$ of as a linear map such that $ D_qX^k=[k]_qX^{k-1}$.



Remark:As always at $ q=1$ we recover the classical definition of the derivative.


It turnes out that there is a property similar to the Leibnitz rule $ ($3$ )$.

Lemma 8  

$\displaystyle D_q(p_1(X)p_2(X))=(D_qf(X))g(X) + f(qX)(D_qg(X))=(D_qf(X))g(qX) + f(X)(D_qg(X)). $


Exercise:Proof the lemma.


The calculus type definition of the usual derivative involves taking a certain limit: one has to consider infinetly small changes of the variable. A nice thing is that in the q-case this definition becomes easy.

Lemma 9  

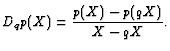
$\displaystyle D_qp(X)=\frac{p(X)-p(qX)}{X-qX}. $


Exercise:Proof the lemma and observe what happens in the limit $ q\to 1$.


In the same spirit, let us define the q-exponential.


Definition:The q-exponential $ E_q(X)$ is defined by the formula

$\displaystyle E_q(X)=1+X+\frac{X^2}{[2]_q^!}+\frac{X^3}{[3]_q^!}+\dots $



Exercise:Prove that $ D_q E_q(X) =E_q(X)$.



Exercise:Let $ YX=qXY$. Prove that $ E_q(X+Y)=E_q(X)E_q(Y)$. Note that we cannot switch factors in the RHS.



Exercise:Let $ YX=qXY$. Prove the q-version of the Taylor expansion formula:

$\displaystyle p(X+Y)=E_q(XD_q^Y)p(Y), $

where $ D_q^Y$ is the q-differention with respect to $ Y$ variable.