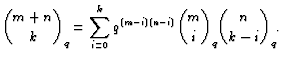Gaussian $ q$-numbers

What we do next was known already to Gauss but the deep meaning of these games became clear much later after invention of quantum mechanics and related objects. In fact we really study ``a free quantum particle on a line''.

Question. What are binomial coefficients?

One possible answer to this question is the following. The binomial coefficients are coefficients in the Newton binomial formula. That is we take to letters $ x,y$, and expand powers of the sum $ x+y$ assuming (usually silently!) that $ xy=yx$ then we find numbers which are called binomial coefficients. Note also that the first binomial coefficient $ {n \choose 1}$ is actually number $ n$ itself.

Consider the ring of polynomials in variables $ X$, $ Y$ such that $ YX=qXY$ for some real number $ q$. These polynomials are again objects of the type

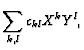
$\displaystyle \sum_{k,l}c_{kl}X^kY^l, $

where $ c_{k,l}$ are some numbers and we add them as usual. However the multiplication changes. Let us consider some examples:

$\displaystyle (XY^2+Y)(X+XY)=XY^2X+XY^2XY+YX+YXY=q^2X^2Y^2+q^2X^2Y^3+qXY+qXY^2, $

$\displaystyle (X+Y)(X-Y)=X^2-Y^2+(q-1)XY. $

Note that if we set $ q=1$ then we get back to good old (classical) multiplication, where $ (x-y)(x+y)=x^2-y^2$.


Definition:The q-binomial coefficients $ {n \choose k}_q$ are coefficients in the expansion of powers of $ (X+Y)^n$,

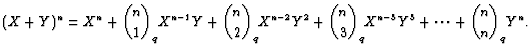
$\displaystyle (X+Y)^n=X^n+{n\choose 1}_qX^{n-1}Y+ {n\choose 2}_qX^{n-2}Y^2+{n\choose 3}_q X^{n-3}Y^3+\dots +{n\choose n}_q Y^n. $

and the quantum number $ [n]_q$ is the first q-binomial coefficient $ [n]_q={n\choose 1}_q$.


First we derive the q-analogs of the Pascal identities.

Lemma 6  

$\displaystyle {n\choose k}={n-1 \choose k}+q^{n-k}{n-1 \choose k-1}, $

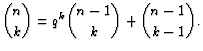
$\displaystyle {n\choose k}=q^k{n-1 \choose k}+{n-1 \choose k-1}. $

Proof. Multiply $ (X+Y)^{n-1}$ by $ (X+Y)$ from the left. Then the term $ X^{n-k}Y^k$ in the result is obtained multiplying the term $ X^{n-k-1}Y^k$ in $ (X+Y)^{n-1}$ by $ X$ and by multiplying the term $ X^{n-k}Y^{k-1}$ in $ (X+Y)^{n-1}$ by $ Y$. Note that in the second case we have to swing $ Y$ to the right through $ X^{n-k}$ which will give a factor $ q^{n-k}$. Now we obtain the first equality by comparing the coefficients in front of $ X^{n-k}Y^k$.

The second equality is proved similarly multiplying $ (X+Y)^{n-1}$ by $ (X+Y)$ from the right. $ \qedsymbol$

Now we are ready to compute the q-binomial coefficients explicitly.

Lemma 7   The q-binomial coefficients are polynomilas in $ q$ with nonnegative integer coefficients, which are equal to usual binomial coefficients when $ q=1$. Explicitly we have

$\displaystyle [n]_q=1+q+q^2+\dots q^{n-1}=\frac{1-q^n}{1-q}, $

$\displaystyle {n\choose k}_q= \frac{[n]_q^!}{[k]_q^![n-k]^!_q}= \frac{(1-q^n)(1-q^{n-1})\dots(1-q^{n-k+1})}{(1-q)(1-q^2)\dots(1-q^k)}, $

where $ [n]_q^!=[1]_q[2]_q\dots[n]_q$.

Proof. Induction on $ n$.


Exercise:Fill out the details.


$ \qedsymbol$

Many identities with bynomial coefficients can be ``deformed'' (``quantized'') to the identities for the q-binomial coefficients. The Pascal identity is one example.

Another example is the Chu-Wandermond identity.


Exercise:Prove that

$\displaystyle {m+n\choose k}_q=\sum_{i=0}^k q^{(m-i)(n-i)}{m\choose i}_q{n\choose k-i}_q. $