| Minicourse: General relativity in spherical symmetry |
|
|
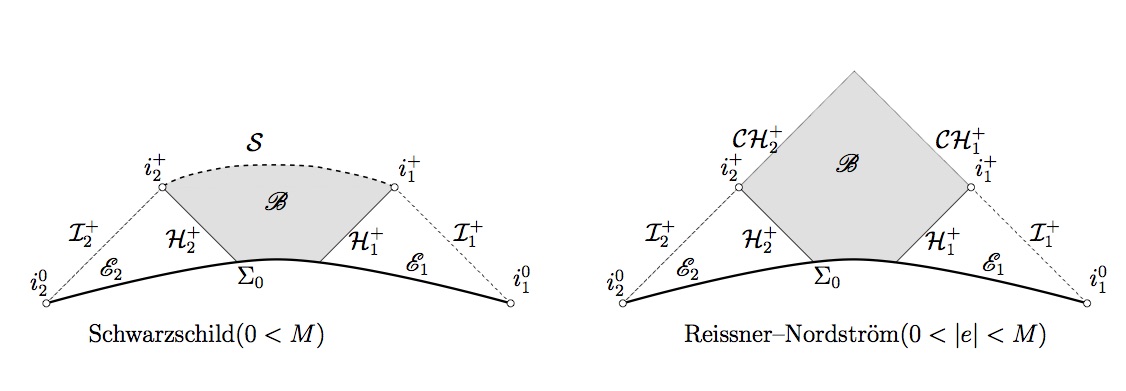
| The first part of this mini-course will be an introduction to general relativity in the simplified setting of spherical symmetry, which allows one to penetrate quickly to the heart of the matter with little technical distractions. Then in the second part, an exposition of the recent proof of the strong cosmic censorship conjecture for the Einstein-Maxwell-Scalar-Field model in spherical symmetry will be given. |