|
You are currently in the topic outlined in red. |
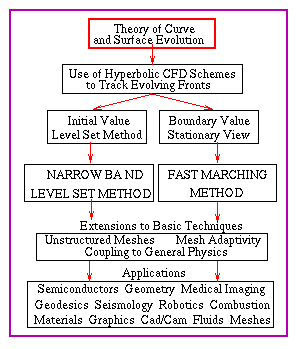
Click on navigable flow chart to go to new topic |
Click on any text to go to a new topic. |
|
You are currently in the topic outlined in red. |

Click on navigable flow chart to go to new topic |
Click on any text to go to a new topic. |
Once this is done, the next step is to consider using numerical technology of shock schemes to directly move an interface.
AbstractWe develop a mathematical theory of flame propagation and analyze the stability of a flame front. We consider a premixed, combustible fluid and model the front between the burnt and unburnt regions as an infinitely thin curve propagating in a direction normal to itself at a constant speed. We assume that the specific volume of a fluid particle increases by a fixed amount when it burns.
Our results show a deep analogy between the equations of flame propagation and hyperbolic systems of conservation laws. We introduce the notion of ignition curves and an entropy condition which enable us to solve the equations of flame propagation in the absence of fluid motion. We prove that any initial front asymptotically approaches a circle as it burns, and that if two fronts start close to each other, they remain so. As the front moves, it may form cusps, which are the result of colliding ignition curves and form in the same way that shocks develop in the solution of hyperbolic systems. These cusps absorb sections of the flame front, destroying information about the initial shape of the front: once a cusp forms, it is impossible to retrieve the initial data by solving the equations of motion backwards in time. We use our theory to discuss the difficulties involved in a numerical approximation to the equations of flame propagation. Finally, we analyze a numerical technique, developed by Chorin, that does not rely on a discrete parameterization of the initial front, and use it to illustrate the results of our theorems.
Download publications
AbstractThe evolution of a front propagating along its normal vector field with curvature dependent speed is considered. We define an "energy-like" quantity of the moving front, the total variation, and prove a general result relating the growth/decay of this energy to the speed. We then study a front moving with speed 1 - epsilon K, where epsilon is a constant and K is the curvature, and show that the curvature term plays a smoothing role in the solution similar to that of viscosity in Burgers equation. For epsilon =0, the solution is seen to blow up, differentiability is lost, and an entropy condition can be formulated to provide an explicit construction for a weak solution beyond blow up time. We numerically solve the equations of motion and show that the solution converges to the constructed weak solution as the curvature smoothing term vanishes. Corners that develop in the propagating front swallow variation in the solution, providing a discontinuous stabilizing mechanism. Finally, we discuss the difficulties involved in numerically solving such problems and a possible remedy is described.
Download publications