Section 7.4: Lagrange Multipliers and Constrained Optimization

A constrained optimization problem is a problem of the form maximize (or minimize) the function $F(x,y)$ subject to the condition $g(x,y) = 0$.

From two to one

In some cases one can solve for $y$ as a function of $x$ and then find the extrema of a one variable function.

That is, if the equation $g(x,y) = 0$ is equivalent to $y = h(x)$, then we may set $f(x) = F(x,h(x))$ and then find the values $x = a$ for which $f$ achieves an extremum. The extrema of $F$ are at $(a,h(a))$.

Example

Find the extrema of $F(x,y) = x^2 y - \ln(x)$ subject to $0 = g(x,y) := 8x + 3y$.

Solution

We solve $y = \frac{-8}{3} x$. Set $f(x) = F(x,\frac{-8}{3} x) = \frac{-8}{3} x^3 - \ln(x)$. Differentiating we have $f'(x) = -8 x^2 - \frac{1}{x}$. Setting $f'(x) = 0$, we must solve $x^3 = \frac{-1}{8}$, or $x = \frac{-1}{2}$. Differentiating again, $f''(x) = -16 x + \frac{1}{x^2}$ so that $f''(\frac{-1}{2}) = 12 > 0$ which shows that $\frac{-1}{2}$ is a relative minimum of $f$ and $(\frac{-1}{2}, \frac{4}{3})$ is a relative minimum of $F$ subject to $g(x,y) = 0$.

A more complicated example

Find the extrema of $F(x,y) = 2y + x$ subject to $0 = g(x,y) = y^2 + xy - 1$.

Solution: Direct, but messy

Using the quadratic formula, we find

$$y = \frac{1}{2} (-x \pm \sqrt{x^2 + 4})$$

Substituting the above expression for $y$ in $F(x,y)$ we must find the extrema of

$$f(x) = \sqrt{x^2 + 4}$$

and

$$\phi(x) = -\sqrt{x^2 + 4}$$

Solution, continued

$$f'(x) = \frac{x}{\sqrt{x^2 + 4}}$$

and

$$\phi'(x) = \frac{-x}{\sqrt{x^2 + 4}}$$

Setting $f'(x) = 0$ (respectively, $\phi'(x) = 0$) we find $x = 0$ in each case. So the potential extrema are $(0,1)$ and $(0,-1)$.

Solution, continued

$$f''(x) = \frac{4}{(\sqrt{x^2 + 4})^3}$$

and

$$\phi''(x) = \frac{-4}{(\sqrt{x^2 + 4})^3}$$

Evaluating at $x = 0$, we see that $f''(0) > 0$ so that $(0,1)$ is a relative minimum and as $\phi''(0) < 0$, $(0,-1)$ is a relative maximum. (even though $F(0,1) = 2 > -2 = F(0,-1)$ !)

Lagrange multipliers

If $F(x,y)$ is a (sufficiently smooth) function in two variables and $g(x,y)$ is another function in two variables, and we define $H(x,y,z) := F(x,y) + z g(x,y)$, and $(a,b)$ is a relative extremum of $F$ subject to $g(x,y) = 0$, then there is some value $z = \lambda$ such that $\frac{\partial H}{\partial x} \vert_{(a,b,\lambda)} = \frac{\partial H}{\parti... ...\vert_{(a,b,\lambda)} = \frac{\partial H}{\partial z}\vert_{(a,b,\lambda)} = 0$.

Example of use of Lagrange multipliers

Find the extrema of the function $F(x,y) = 2y + x$ subject to the constraint $0 = g(x,y) = y^2 + xy - 1$.

Solution

Set $H(x,y,z) = F(x,y) + z g(x,y)$. Then

$$\begin{eqnarray*} \frac{\partial H}{\partial x} & = & 1 + zy \\ \frac{\partial ... ... + 2zy + zx \\ \frac{\partial H}{\partial z} & = & y^2 + xy - 1 \end{eqnarray*}$$

Solution, continued

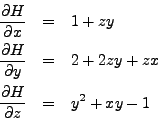
Setting these equal to zero, we see from the third equation that $y \neq 0$, and from the first equation that $z = \frac{-1}{y}$, so that from the second equation $0 = \frac{-x}{y}$ implying that $x = 0$. From the third equation, we obtain $y = \pm 1$.

Another Example

Find the potential extrema of the function $f(x,y) = x^2 + 3xy + y^2 - x + 3 y$ subject to the constraint that $0 = g(x,y) = x^2 - y^2 + 1$.

Solution

Set $F(x,y,\lambda) := f(x,y) + \lambda g(x,y)$. Then

$$\frac{\partial F}{\partial x} = 2x + 3y - 1 + 2 \lambda x$$ (1)

$$\frac{\partial F}{\partial y} = 3x + 2y + 3 + 2 \lambda y$$ (2)

$$\frac{\partial F}{\partial \lambda} = x^2 - y^2 + 1$$ (3)

Solution, continued

Set these all equal to zero.

Multiplying the first line by $y$ and the second by $x$ we obtain:

$$\begin{eqnarray*} 0 &=& 2xy + 3y^2 -y + 2 \lambda xy \\ 0 & =& 2xy + 3x^2 + 3x + \lambda xy \ \end{eqnarray*}$$

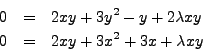
Subtracting, we have

$$\begin{eqnarray*}\ 0 & = & 3(x^2 - y^2) + 3x - y \end{eqnarray*}$$

Solution, continued

As $0 = x^2 - y^2 + 1$, we conclude that $y = 1 -3x$. Substituting, we have $0 = x^2 - (1 - 3x)^2 + 1 = x^2 - 9x^2 + 6x - 1 + 1 = -8x^2 + 6x = x(6 - 8x)$.

So the potential extrema are at $(0,1)$ or $(\frac{3}{4},\frac{-1}{4})$.