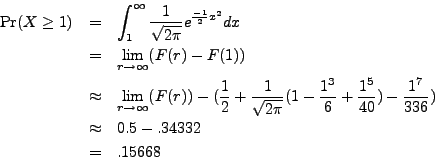Given a positive constant ![]() , the exponential density
function (with parameter
, the exponential density
function (with parameter ![]() ) is
) is
Let ![]() be a continuous random variable with
an exponential density function with parameter
be a continuous random variable with
an exponential density function with parameter ![]() .
.
Integrating by parts with ![]() and
and
![]() so that
so that
![]() and
and
![]() , we find
, we find
![\begin{eqnarray*}
E(X) & = & \int_{-\infty}^\infty x f(x) dx \\
& = & \int_{0}...
...e^{-kx} - \frac{1}{k} e^{-kx}]\vert_{0}^r \\
& = & \frac{1}{k}
\end{eqnarray*}](img9.png)
Integrating by parts with ![]() and
and
![]() so that
so that
![]() and
and
![]() , we have
, we have
![\begin{eqnarray*}
\int_0^\infty x^2 e^{-kx} dx & = & \lim_{r \to \infty}( [- x^2...
...-kx} - \frac{2}{k^2} e^{-kx}]\vert_0^r) \\
& = & \frac{2}{k^2}
\end{eqnarray*}](img12.png)
So,
![]() .
.
Exponential random variables (sometimes) give good models for the time to failure of
mechanical devices. For example, we might measure the number of miles traveled by a
given car before its transmission ceases to function. Suppose that this distribution
is governed by the exponential distribution with mean ![]() . What is the probability
that a car's transmission will fail during its first
. What is the probability
that a car's transmission will fail during its first ![]() miles of operation?
miles of operation?
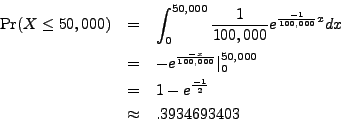
The normal density function with mean ![]() and standard deviation
and standard deviation ![]() is
is
As suggested, if ![]() has this density, then
has this density, then ![]() and
and
![]() .
.
The standard normal density function is the normal density function with
![]() . That is,
. That is,
Let
![]() be the
standard normal density function and let
be the
standard normal density function and let
![]() be the standard normal cumulative distribution function.
be the standard normal cumulative distribution function.
We compute a Taylor series expansion,
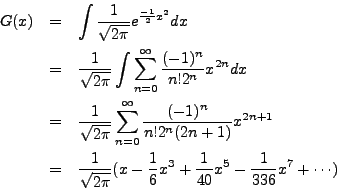
So
![]() for some
for some ![]() .
As
.
As ![]() is the expected value, we need
is the expected value, we need
![]() .
.
If the continuous random variable ![]() is normally distributed, what is the probability that
it takes on a value of more than a standard deviations above the mean?
is normally distributed, what is the probability that
it takes on a value of more than a standard deviations above the mean?
Via a change of variables, we may suppose that ![]() is normally distributed
with respect to the standard normal distribution. Let
is normally distributed
with respect to the standard normal distribution. Let ![]() be the
cumulative distribution function for the standard normal distribution.
be the
cumulative distribution function for the standard normal distribution.