There are several tests for the convergence or divergence of infinite series with all positive terms. We consider two.
If ![]() is a function with
is a function with ![]() a decreasing continuous function
defined for all numbers
a decreasing continuous function
defined for all numbers ![]() , then the infinite series
, then the infinite series
![]() converges if and only if the integral
converges if and only if the integral
![]() converges.
converges.
Use the integral test to determine whether or not
![]() converges.
converges.
Indeed, it does not as
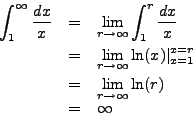
Does the series
![]() converge?
converge?
Consider
![]() . We compute
. We compute
![]() which is
negative for all
which is
negative for all ![]() . Thus,
. Thus, ![]() is decreasing.
is decreasing.
We compute using integration by parts with ![]() so that
so that ![]() and
and
![]() so that
so that ![]() ,
,
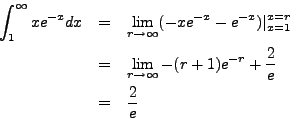
Hence,
![]() converges.
converges.
If
![]() and
and
![]() are two sequences
of positive numbers for which
are two sequences
of positive numbers for which ![]() for every
for every ![]() , then
, then
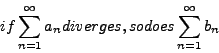
while
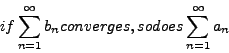
moreover,
![]() .
.
Does the series
![]() converge?
converge?
Yes:
![]() for every
for every ![]() . We
know
. We
know
![]() . Hence,
. Hence,
![]() converges and is at most
converges and is at most ![]() .
.