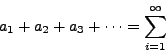
An infinite series is a ``sum'' of the form
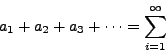
Given a sequence
![]() of numbers, the
of numbers, the ![]() partial
sum of this sequence is
partial
sum of this sequence is
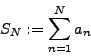
We define the infinite series
![]() by
by
For the sequence
![]() , we have
, we have
![]() .
Thus,
.
Thus,
![]() is divergent.
is divergent.
For the sequence
![]() , we have
, we have ![]() ,
, ![]() ,
, ![]() , etc.
In general,
, etc.
In general, ![]() for
for ![]() odd and
odd and ![]() for
for ![]() even. Thus,
even. Thus,
![]() is divergent.
is divergent.
If one computes the partial sums for
![]() one finds
one finds
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . In fact,
. In fact,
![]() , so
that
, so
that
![]() diverges, though we will
see why only later.
diverges, though we will
see why only later.
If one computes the partial sums for
![]() , then one
obtains
, then one
obtains
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
In fact,
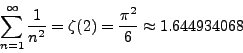
The series
![]() is an example of a geometric
series. Computing, we find
is an example of a geometric
series. Computing, we find ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() . In fact,
. In fact, ![]() .
.
A geometric series is a series of the form
In the above case
![]() .
.
If
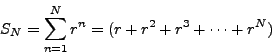
then
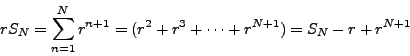
Subtracting ![]() from both sides, we obtain
from both sides, we obtain
Hence,
So
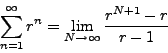
provided that the limit on the right exists.
If ![]() , then
, then
![]() , so that
, so that
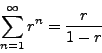
If ![]() , then
, then
![]() does not exist, so
does not exist, so
![]() diverges.
diverges.
Finally, in the case that ![]() , we have already seen that the series
diverges.
, we have already seen that the series
diverges.
Compute the following sums
In the first case, we may write the sum as
![]() .
So, the sum is
.
So, the sum is
![]() .
.
In the second case, we may write the sum as
![]() so that this sum is
so that this sum is
![]() .
.