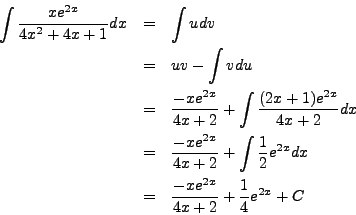Perform the following indefinite integration.
Often, one finds two functions ![]() and
and ![]() so that the
integrand may be written as
so that the
integrand may be written as ![]() where
where ![]() .
If we succeed in so doing, then from the equality
.
If we succeed in so doing, then from the equality
If ![]() is easier to evaluate than is
is easier to evaluate than is ![]() , then the
method succeeds.
, then the
method succeeds.
Take ![]() and
and ![]() so that
so that
![]() and
and ![]() . Then,
. Then,
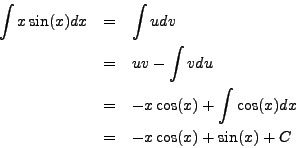
Integrate:
Take ![]() and
and ![]() so that
so that ![]() and
and ![]() .
.
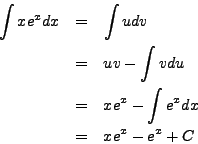
Integrate
Set ![]() and
and ![]() so that
so that ![]() and
and
![]() .
.
Then
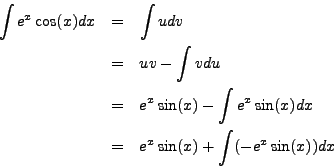
Set ![]() and
and ![]() so that
so that ![]() and
and
![]() .
.
Then
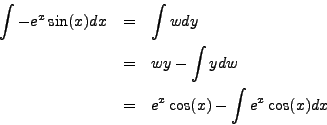
Substituting, we have
Adding
![]() and dividing by
and dividing by ![]() gives
gives
Integrate
Set ![]() and
and ![]() so that
so that
![]() and
and ![]() .
.
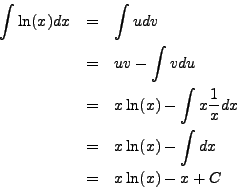
Integrate
Note that
![]() . Via the substitution
. Via the substitution ![]() (with
(with
![]() ) we find that
) we find that
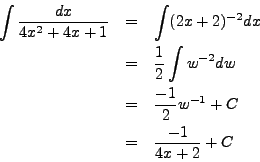
Set ![]() and
and
![]() (so that
(so that
![]() and
and
![]() ).
).