First, try to simplify the integrand, in this case, with one of the laws of exponents
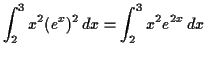
this is a product but not in the form of a substitution, so try integration by parts. Now the derivative of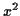 is simpler
and the antiderivative is more complicated,
while the derivative and antiderivatives of
is simpler
and the antiderivative is more complicated,
while the derivative and antiderivatives of 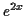 are about the same in complexity, so try
are about the same in complexity, so try
![\begin{displaymath}\begin{array}[t]{r@{}l@{\quad}r@{}l}
f (x) &= x^2 & g(x) &= ...
...\\
f'(x) &= 2x & G(x) &= \tfrac{1}{2}e^{2x} \\
\end{array}\end{displaymath}](img4.gif)
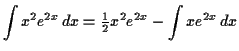
To do the resulting integral, again integrate by parts![\begin{displaymath}\begin{array}[t]{r@{}l@{\quad}r@{}l}
f (x) &= x & g(x) &= e^...
... \\
f'(x) &= 1 & G(x) &= \tfrac{1}{2}e^{2x} \\
\end{array}\end{displaymath}](img6.gif)
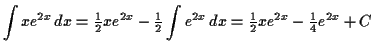
Finally, we put it all together with the limits,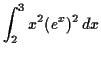
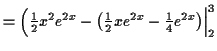
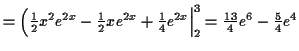
Again, first simplify the integrand
![$\displaystyle \int_0^1 \dfrac{\ln (\sqrt[4]{x})}{x} \,d x = \int_0^1 \dfrac{\ln (x^{1/4})}{x} \,d x = \int_0^1 \dfrac{\ln x}{4x} \,d x$](img11.gif)
Note that this is an improper integral because both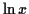 and
and
 are not defined at
are not defined at 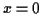 .
To do the integral, note that the derivative of
.
To do the integral, note that the derivative of 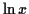 is
is
 ,
so do substitution with
,
so do substitution with 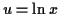 and
and
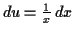
![$\displaystyle \int \dfrac{\ln (\sqrt[4]{x})}{x} \,d x = \tfrac{1}{4} \int u \,d u = \tfrac{1}{8} u^2 + C = \tfrac{1}{8} (\ln x)^2 + C$](img17.gif)
But we need to plug in the lower limit as an improper integral![$\displaystyle \int_0^1 \dfrac{\ln (\sqrt[4]{x})}{x} \,d x$](img18.gif)
![$\displaystyle = \lim_{a \to 0^+} \int_a^1 \dfrac{\ln (\sqrt[4]{x})}{x} \,d x$](img19.gif)
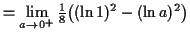
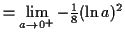
Note that .
To evaluate the limit, note that as
.
To evaluate the limit, note that as  from the positive side,
from the positive side,
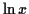 becomes very big negative,
so
becomes very big negative,
so 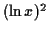 becomes very big positive,
and
becomes very big positive,
and
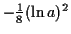 becomes very big negative.
Thus the integral diverges, and we say
becomes very big negative.
Thus the integral diverges, and we say
![$\displaystyle \int_0^1 \dfrac{\ln(\sqrt[4]{x})}{x} \,d x= -\infty$](img26.gif)
There are other ways to do the integral correctly. These all give the same answer after simplifying with laws of logarithms and exponents.
Substitution with
![$ u = \ln (\sqrt[4]{x}) = \ln \bigl(x^{1/4}\bigr)$](img27.gif) and
and
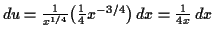
![$\displaystyle \int \dfrac{\ln(\sqrt[4]{x})}{x} \,d x = 4 \int u \,d u= 2 u^2 + C = 2 \bigl(\ln(\sqrt[4]{x})\bigr)^2 + C$](img29.gif)
Do not forget the chain rule in computing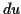 .
.
Integration by parts with
![\begin{displaymath}\begin{array}[t]{r@{}l@{\quad}r@{}l}
f (x) &= \ln(\sqrt[4]{x...
... \\
f'(x) &= \tfrac{1}{4x} & g(x) &= \ln(x) \\
\end{array}\end{displaymath}](img31.gif)
![$\displaystyle \int \dfrac{\ln(\sqrt[4]{x})}{x} \,d x$](img32.gif)
![$\displaystyle = \ln(\sqrt[4]{x}) \ln(x) - \int \dfrac{\ln x}{4x} \,d x$](img33.gif)
![$\displaystyle = \ln(\sqrt[4]{x}) \ln(x) - \tfrac{1}{8}(\ln x)^2 + C$](img34.gif)
where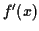 and
and
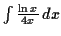 are as calculated above.
are as calculated above.
Integrating by parts don't work the other way because we don't know the antiderivative of
![$ \ln(\sqrt[4]{x})$](img37.gif) .
.
Same as above but integrate
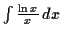 by parts
by parts
![\begin{displaymath}\begin{array}[t]{r@{}l@{\quad}r@{}l}
f (x) &= \ln x & G(x) &...
...x} \\
f'(x) &= \tfrac{1}{x} & g(x) &= \ln x \\
\end{array}\end{displaymath}](img39.gif)
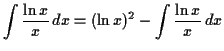
Note that the two integrals are the some, so moving them to the same side gives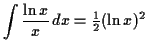
Integrating by parts the other way don't work. It gives
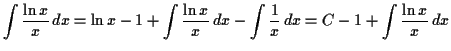
because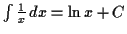 .
This don't tell us anything as indefinite integrals differ by a constant.
.
This don't tell us anything as indefinite integrals differ by a constant.
There are a couple ways to do
![$ \int \cos(x) \sin(x) \sqrt[3]{\sin(x) + 2} \,d x$](img44.gif)
The integrand contains a single
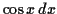 and many
and many  , whose derivative is
, whose derivative is 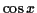 ,
so try the substitution
,
so try the substitution
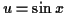 and
and
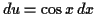
![$\displaystyle \int \cos(x) \sin(x) \sqrt[3]{\sin(x) + 2} \,d x = \int u (u + 2)^{1/3} \,d u$](img50.gif)
then all we can do next is integration by parts. Since the derivative of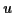 is the simplest,
we should try
is the simplest,
we should try
![\begin{displaymath}\begin{array}[t]{r@{}l@{\quad}r@{}l}
f (u) &= u & g(u) &= (u...
...'(u) &= 1 & G(u) &= \tfrac{3}{4} (u + 2)^{4/3} \\
\end{array}\end{displaymath}](img52.gif)
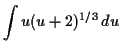
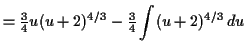
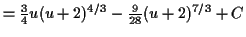
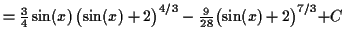
Note that the variable is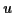 ,
which is converted back to
,
which is converted back to  at the end.
at the end.
Instead, we can take a bigger substitution without changing its derivative
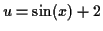 and
and
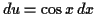
![$\displaystyle \int \cos(x) \sin(x) \sqrt[3]{\sin(x) + 2} \,d x = \int (u - 2) u^{1/3} \,d u$](img59.gif)
Note that we used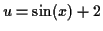 to replace
to replace
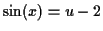 .
This is necessary because
.
This is necessary because  depends on
depends on 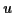 because
because 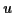 depends on
depends on  ,
and when we integrate with respect to
,
and when we integrate with respect to 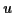 we need to know exactly how
we need to know exactly how 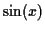 changes with respect to
changes with respect to 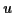 .
There are two ways to do the integral:
.
There are two ways to do the integral:
Integrate by parts, with
 chosen to have the simplest derivative
chosen to have the simplest derivative
![\begin{displaymath}\begin{array}[t]{r@{}l@{\quad}r@{}l}
f (u) &= u - 2 & g(u) &...
...\
f'(u) &= 1 & G(u) &= \tfrac{3}{4} u^{4/3} \\
\end{array}\end{displaymath}](img63.gif)
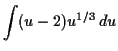
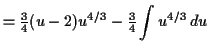
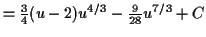
which is the same as before when we put in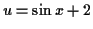 .
.
Or, we can multiply it out and use the laws of exponents to simplify
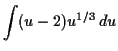
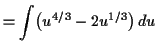
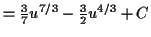
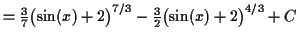
and we can see this is the same by multiplying out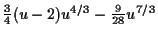
We can also try integration by parts first, but it's harder to see how to choose
 and
and 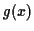 without before using substitution to simplify the integral.
For
without before using substitution to simplify the integral.
For 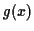 , we need something we can integrate to
, we need something we can integrate to 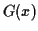
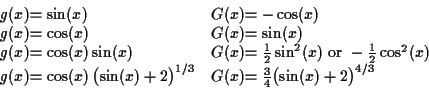
The last case corresponds to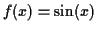 and
and
 .
It is the only one where
.
It is the only one where 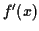 is no more complicated than
is no more complicated than  and in fact, the only one that can be done by integrating by parts,
giving
and in fact, the only one that can be done by integrating by parts,
giving
![$\displaystyle \int \cos(x) \sin(x) \sqrt[3]{\sin(x) + 2} \,d x$](img77.gif)
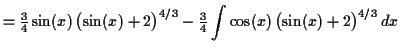
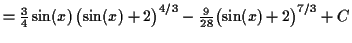
To approximate
![]() using Simpson's rule with
using Simpson's rule with ![]() ,
divide the interval
,
divide the interval ![]() into
into ![]() pieces
bounded by the points
pieces
bounded by the points ![]() ,
, ![]() and
and ![]() each of size
each of size
![]() .
Let
.
Let
![]() , then the trapezoid rule approximation is
, then the trapezoid rule approximation is
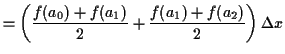 |
||
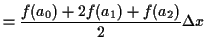 |
||
The midpoints are
The Simpson rule approximation is
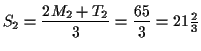 |
Or, with the other formula,
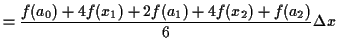 |
||
To solve the differential equation
![]() ,
with initial condition
,
with initial condition
![]() , use separation of variables.
First, there is a constant solution
, use separation of variables.
First, there is a constant solution ![]() ,
but that doesn't satisfy the initial condition. Then
,
but that doesn't satisfy the initial condition. Then
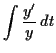 |
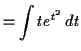 |
|
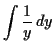 |
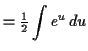 |
|
where
The initial condition requires
so
A Euler's method problem should be on the final.
Start at
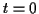 at the given initial value
at the given initial value 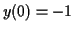 .
There, the slope
.
There, the slope
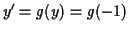 is positive, so
is positive, so 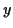 increases.
Thus we move right (the positive direction) along the
increases.
Thus we move right (the positive direction) along the 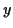 -axis,
and we find that the slope
-axis,
and we find that the slope 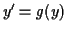 decreases
until it reaches 0 at
decreases
until it reaches 0 at  .
Thus the solution
.
Thus the solution 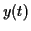 starts from
starts from 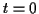 at
at 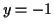 with a positive slope,
and concaves up and becomes asymptotic to
with a positive slope,
and concaves up and becomes asymptotic to  .
This is (d).
.
This is (d).
Start at
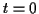 at the given initial value
at the given initial value 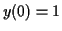 .
There, the slope
.
There, the slope
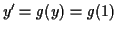 is negative, so
is negative, so 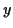 decreases.
Thus we move left (the negative direction) along the
decreases.
Thus we move left (the negative direction) along the 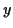 -axis,
and we find that the slope
-axis,
and we find that the slope 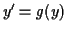 increases
(gets closer to 0) until it reaches 0 at
increases
(gets closer to 0) until it reaches 0 at  .
Thus the solution
.
Thus the solution 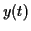 starts from
starts from 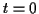 at
at 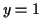 with a negative slope,
and concaves down and becomes asymptotic to
with a negative slope,
and concaves down and becomes asymptotic to  .
This is (b).
.
This is (b).
Let ![]() be the amount of compound A,
then the rate at which A transforms to B is
be the amount of compound A,
then the rate at which A transforms to B is ![]() .
The rate is negative
because the amount of A decreases as it is transformed to B,
but that's okay.
``The rate is proportional to the cube of B,''
and the other conditions translates to
.
The rate is negative
because the amount of A decreases as it is transformed to B,
but that's okay.
``The rate is proportional to the cube of B,''
and the other conditions translates to
for some (negative) constant
 |
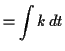 |
|
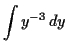 |
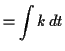 |
|
Initially, there are
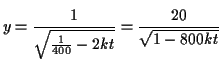 |
After
The solution is
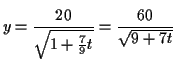 |
The amount of A after